Plangeometriske figurer
Vi skal plassere firkanter i et hierarki. Det kan se noe slik ut:

-
- Vi skal finne arealet til et trapes der de to parallelle sidene er henholdsvis 5 og 8 cm og høyden er 6 cm.
Vi bruker formelen for arealet av et trapes, $A={{\displaystyle (a+b) \cdot h}\over{\displaystyle 2}}$, der a og b er de parallelle sidene og h høyden og får$A={{\displaystyle (5+8) \cdot 6}\over{\displaystyle 2}} cm^2 = 39 \, cm^2$
- Vi vet at et trapes har areal 26 cm2, at de to parallelle sidene er 7 og 6 cm. og skal finne trapesets høyde.
Vi bruker vanlige algebra-regler til å regne om formelen slik at vi får høyden alene på venstre side av likhetstegnet: $h={{\displaystyle 2A}\over{\displaystyle a + b}}$, setter inn og får
$h={{\displaystyle 2 \cdot 26 }\over{\displaystyle 7 + 6 }} cm = 4 \, cm$
- Vi skal finne arealet til et trapes der de to parallelle sidene er henholdsvis 5 og 8 cm og høyden er 6 cm.
Trigonometri
Det er oppgitt at i en rettvinklet trekant er hypotenusen 13 cm og den ene kateten 12 cm, og vi skal finne ut hvor lang den andre kateten er.
Kaller vi hypotenusen c og katetene a og b, sier Pytagoras′ setning at c2 = a2 + b2.
Vi regner om slik at den ene kateten blir stående alene til venstre for likhetstegnet:
a2 = b2 − c2
Setter vi inn, får vi a2=132 − 122 = 25. Det vil si at $a=\sqrt{25} = 5$.
Den andre kateten er 5 cm.
I en rettvinklet trekant med navn som i figuren under, er det oppgitt at vinkelen v = 42° og d = 10, og vi skal finne lengdene til c og e.

Vi har at cosinus til en vinkel i en rettvinklet trekant er lik forholdet mellom hosliggende katet og hypotenusen: $\cos v = {\large \frac{c}{d}}$.
Regner vi om slik at vi får c alene på venstre side av likhetstegnet, blir det
c = d · cos v.
Vi finner cos 42° ≈ 0,74 på en kalkulator eller i GeoGebra e.l., setter inn og får
c ≈ 10 · 0,74 = 7,4.
Vi har at sinus til en vinkel i en rettvinklet trekant er lik forholdet mellom motstående katet og hypotenusen:
$\sin v = {\large \frac{e}{d}}$.
Regner vi om slik at vi får e alene på venstre side av likhetstegnet, blir det
e = d · sin v.
Vi finner sin 42° ≈ 0,67, setter inn og får
e ≈ 10 · 0,67 = 6,7
Her kunne vi også brukt Pytagoras′ setning og fått
$e^2 = d^2 − c^2 \approx 10^2 − 7{,}4^2 = 45{,}24 \Rightarrow e \approx \sqrt{45{,}24 } \approx 6{,}7$
c er om lag 7,4 cm lang og e er om lag 6,7 cm lang.
I trekanten under vet vi at sidelengdene a = 7 og c = 9, og skal bruke trigonometri til å finne vinkelen A.

Vi vet at sinus til en vinkel er lik motstående katet over hypotenusen, så vi får at
$\sin A = \frac{\displaystyle a}{\displaystyle c} = {\large \frac{7}{9}} \approx 0{,}78$.
A = sin−1 0,78 ≈ 51,3°.
Vi får da at A = sin−1 0,78 ≈ 51,3°.
Så skal vi kontrollere at vinkelsummen i trekanten er 180°, når vi vet at B er om lag 38,7°.
Vi får 90° + 38,7° + 51,3°= 180°.
Vi skal undersøk om sammenhengene
$\cos v = \sin(90^ \circ − v)$
$\tan v = \frac{\displaystyle \sin v}{\displaystyle \cos v}$
er riktige for vinklene 0, 30, 45, 60 og 90 grader, slik de er vist i tabellen under.
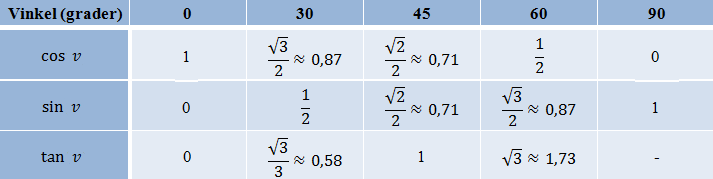
Vi ser at
$\cos 0^\circ = \sin(90^\circ − 0^\circ) = \sin 90^\circ = 1$
$\cos 30^\circ = \sin(90^\circ − 30^\circ) = \sin 60^\circ = {\large \frac{\sqrt 3}{2}}$
$\cos 45^\circ = \sin(90^\circ − 45^\circ) = \sin 45^\circ = {\large \frac{\sqrt 2}{2}}$
$\cos 60^\circ = \sin(90^\circ − 60^\circ) = \sin 30^\circ = {\large \frac{1}{2}}$
$\cos 90^\circ = \sin(90^\circ − 90^\circ) = \sin 0^\circ = 0$
${\large \frac{\sin 0^\circ}{\cos 0^\circ}}= {\large \frac{0}{1}} = 0 = \tan 0^\circ$
${\large \frac{\sin 30^\circ}{\cos 30^\circ}}= {\large \frac{\frac{1}{2}}{\frac{\sqrt 3}{2}}} = {\large \frac{1}{\sqrt 3}} = {\large \frac{\sqrt 3}{3}} = \tan 30^\circ$
${\large \frac{\sin 45^\circ}{\cos 45^\circ}}= {\large \frac{\frac{\sqrt 2}{2}}{\frac{\sqrt 2}{2}}} = 1= \tan 45^\circ$
${\large \frac{\sin 60^\circ}{\cos 60^\circ}}= {\large \frac{\frac{\sqrt 3}{2}}{\frac{1}{2}}} = \sqrt 3 = \tan 60^\circ$
${\large \frac{\sin 90^\circ}{\cos 90^\circ}}= {\large \frac{1}{0}}$. Denne verdien er udefinert.
Alt stemmer med tabellen.
Vektorregning
Vi har punktene G = (0, 4), L = (−2, 2), O = (2, 3) og R = (4, 4), og skal beregne koordinatene til vektorene $\vec{GL}$ og $\vec{OR}$.
Vi finner koordinatene til vektorer ved å trekke x– og y-koordinatene til startpunktet fra henholdsvis x– og y-koordinatene til sluttpunktet, så vi får
$\vec{GL} = [−2 − 0, 2 − 4] = [−2, −2]$
$\vec{OR} = [4 − 2, 4 − 3] = [2, 1]$
Vi har vektorene $\vec{a} = [−3, 2]$, $\vec{b} = [4, 2]$ og $\vec{c} = [−1, −3]$ og skal beregne
$\vec{a} + \vec{b} + \vec{c}$.
Vi får
$\vec{a} + \vec{b} + \vec{c} = [−3 + 4 + (−1), 2 + 2 + (−3)] = [0, 1]$
Vi skal beregne $|\vec{b}|$ når $\vec{b} = [12, 5]$
Vi får
$|\vec{b}| = \sqrt{12^2 + 5^2} = \sqrt{169} = 13$
Vi har vektorene $\vec{a} = [3,1]$ og $\vec{b} = [−2,3]$ og skal beregne
$2\vec{a} + 4 \vec{b}$
Vi får
$2\vec{a} + 4 \vec{b} = 2[3,1] + 4[−2,3] = [6,2] + [−8,12]=[−2,14]$
Vi skal beregne prikkproduktet til vektorene $\vec{a} = [4,2]$ og $\vec{b} = [−8,−4]$
Vi får
$\vec{a} \cdot \vec{b} = 4 \cdot (−8) + 2 \cdot (−4) = −40$
Vi skal beregne prikkproduktet av vektorene fra oppgave 5, $\vec{a} = [4,2]$ og $\vec{b} = [−8,−4]$ ved å benytte at vinkelen mellom vektorene er $180^\circ$.
Vi vet at
cos 180° = −1
og beregner
$|\vec{a}| = \sqrt{4^2 + 2^2} = \sqrt{20}$
og
$|\vec{b}| = \sqrt{(−4)^2 + (−8)^2} = \sqrt{80}$
Så prikkproduktet blir
$\vec{a} \cdot \vec{b} =\sqrt{20} \cdot \sqrt{80} \cdot (−1) = \sqrt{1600} \cdot(−1) = −40$
Som er det samme som vi fikk i oppgave 5.
Vi skal finne vinkelen mellom vektorene $\vec{a} = [2,−1]$ og $\vec{b} = [1,3]$.
Vi har at (I)
$\vec{a} \cdot \vec{b} = a_x \cdot b_x + a_y \cdot b_y = 2\cdot 1 + (−1) \cdot 3 = −1$
Samtidig har vi at (II)
$\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b} | \cos \theta = \sqrt{2^2 + (−1)^2} \cdot \sqrt{1^2 + 3^2} \cdot \cos \theta = \\
\sqrt{5} \cdot \sqrt{10} \cdot \cos \theta = \sqrt{50} \cdot \cos \theta$
Setter vi sammen I og II, får vi
$−1 =\sqrt{50} \cos \theta\Rightarrow \cos \theta = {\large \frac{−1}{\sqrt{50}}}$
Så
$\theta = \cos^{−1}{\Big({\large \frac{−1}{\sqrt{50}}}}\Big) \approx 98{,}13^\circ$
Dette er illustrert under.

Vi skal beregne projeksjonen av $\vec{a} = [−3, 2]$ på $\vec{b} = [4, 1]$
Vi får
$\vec{a} \cdot \vec{b} = a_x \cdot b_x + a_y \cdot b_y = −3\cdot 4+ 2 \cdot 1 = −10$
og
$\vec{b} \cdot \vec{b} = b_x \cdot b_x + b_y \cdot b_y = 4 \cdot 4 + 1 \cdot 1 = 17$
Så
$\vec{a_b} = {\large \frac{−10}{17}}[4,1] \approx[−2{,}35, −0{,}59]$
Dette er illustrert under.

Polarkoordinater
Vi skal angi punktet $(4,3)$ i polarkoordinater. Da setter vi x = 4 og y = 3 inn i $r = \sqrt{x^2 + y^2}$ og $\theta = \tan^{−1}{\large \frac{y}{x}}$ og får:
$r = \sqrt{4^2 + 3^2} = 5$
og
$\theta = \tan^{−1}{\large \frac{3}{4}} \approx 37^\circ$
Så punktet blir (5, 37°)
Vi skal angi punktet (2, 60°) i kartesiske koordinater. Da setter vi r = 2 og θ = 60° inn i x = r · cos θ og y = r · sin θ og får:
$x = 2 \cdot \cos 60^\circ = 2 \cdot {\large \frac{1}{2}} = 1$
og
$y = 2 \cdot \sin60^\circ = 2 \cdot {\large \frac{\sqrt 3}{2}} = \sqrt3$
Så punktet blir $(1, \sqrt 3)$