Stikkord: rettvinklet trekant

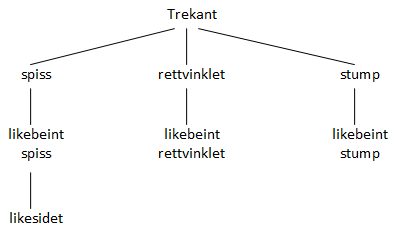
Ordet trigonometri kommer av det greske trigonon, som betyr tre vinkler, og metro, som betyr måling. Trigonometri brukes i sammenheng med beregning av sider og vinkler i trekanter.

I funksjonsartikkelen om trigonometriske funksjoner ble vi kjent med funksjonene sinus, cosinus og tangens. Nå skal vi se hvordan disse kan benyttes til å bestemme trekanter, det vil si å finne størrelsene på alle vinklene og lengden av alle sidene i trekanten.

Trigonometri i rettvinklede trekanter

I en rettvinklet trekant er en av vinklene er 90°. Sidene som ligger inntil til den rette vinkelen kalles kateter, mens den motstående siden kalles hypotenusen. Dette er illustrert i figuren under.

Pytagoras′ setning

Pytagoras′ setning er oppkalt etter den greske matematikeren Pytagoras. Setningen angir en sammenheng mellom sidelengdene i en rettvinklet trekant, og sier at summen av kvadratene av katetene er lik kvadratet av hypotenusen. Kaller vi sidene a, b og c som på figuren over, har vi altså at

a² + b² = c²

Det finnes en mengde forskjellige typer bevis for Pytagoras setning. Se for eksempel denne demonstrasjonen med vanntanker fra Vitensenteret i Arendal.

Oppgave 1:

I en rettvinklet trekant er hypotenusen 13 cm og den ene kateten 12 cm. Hvor lang er den andre kateten?

Se løsningsforslag

Trigonometriske funksjoner

Pytagoras′ setning gir oss hjelp til å finne lengden av den tredje siden i en rettvinklet trekant når to av de andre er kjent. Men den gir ingen hjelp med å finne vinklene. Til det trenger vi de trigonometriske funksjonene, som vi kaller sinus, cosinus og tangens. Dette er funksjoner i ordets egentlige forstand, og vi studerer dem i funksjonsartikkelen om trigonometriske funksjoner, men her nøyer vi oss med å si at de kan brukes til å uttrykke forholdstall i trekanter. Fordi funksjonsverdiene kan finnes med en kalkulator eller i et dataprogram som Excel eller GeoGebra, har vi derved et redskap til å beregne størrelsen på en trekants vinkler.

De to vinklene i en rettvinklet trekant som ikke er 90°, vil ligge mellom en katet og hypotenusen. Kateten som ligger inntil vinkelen, kalles hosliggende katet, den andre kalles motstående katet. Dette er illustrert for vinkelen v i figuren under.

Det er da slik at 

• sinus til en vinkel er lik lengden av motstående katet dividert med lengden av hypotenusen.
• cosinus til en vinkel er lik lengden av hosliggende katet dividert med lengden av hypotenusen.
• tangens til en vinkel er lik lengden av motstående katet dividert med lengden av hosliggende katet.

Vi forkorter gjerne funksjonsnavnene til sin, cos og tan. Med referanse til figuren over har vi altså at

$\fbox{$\begin{align} \sin v &= \frac{\displaystyle b}{\displaystyle c} \\
&\, \\
\cos v &= \frac{\displaystyle a}{\displaystyle c} \\
&\, \\
\tan v &= \frac{\displaystyle b}{\displaystyle a} \end{align}$}$

Kjenner vi størrelsen til en vinkel i en rettvinklet trekant og lengden til en av sidene, kan vi ved hjelp av disse formlene beregne lengdene til de to andre sidene. Sinus, cosinus og tangens til en vinkel finner vi ved hjelp av en kalkulator eller et dataprogram som Excel eller GeoGebra.

Eksempel 1:

I en rettvinklet trekant med navn som i figuren over, har vi at vinkelen v = 50°, at sidelengden a=7, og vi skal bruke trigonometriske funksjoner til å finne sidelengdene b og c.

Fra lista med formler ser vi at $\tan v =  \frac{\displaystyle b}{\displaystyle a}$, altså er b = a · tan v.

Vi setter inn de oppgitte verdiene og får

b = 7 · tan 50° ≈ 7 · 1,19 ≈ 8,33.

Fra lista med formler ser vi at $\cos v = \frac{\displaystyle a}{\displaystyle c}$, altså er $c = \frac{\displaystyle a}{\displaystyle \cos v}$.

Vi setter inn de oppgitte verdiene og får

$c = {\large \frac{7}{\cos 50^\circ}} \approx {\large \frac{7}{0{,}64}} \approx 10{,}89$.

Her brukte vi en kalkulator til å finne tan 50° ≈ 1,19 og cos 50° ≈ 0,64.

I eksempel 1 kunne vi også brukt formelen $\sin v = \frac{\displaystyle b}{\displaystyle c}$ til å beregne c, for vi hadde jo allerede beregnet b. Imidlertid inneholder b en avrundingsunøyaktighet, mens a er oppgitt til å være akkurat 7. Derfor er det et bedre valg å bruke at $\cos v = \frac{\displaystyle a}{\displaystyle c}$, slik vi har gjort. Når vi har flere alternative utregningsmetoder, vil det ofte være et godt valg å bruke den som gir minst unøyaktighet.

I eksempel 1 kunne vi naturligvis også beregnet c ved hjelp av Pytagoras′ setning:

c² = a² + b² ≈ 7² + 8,33² ≈ 118,39 ⇒ c ≈ 10,88.

Som er det samme vi fant i eksempel 1, med unntak av en avrundingsunøyaktighet.

Windows har en kalkulator vi kan få fram ved å skrive «Kalkulator i Windows-menyen. Velger vi så «Vitenskapelig» i menyen øverst til venstre på kalkulatoren, ser den ut som vist under. Her har vi markert knappene for de trigonometriske funksjonene, og knappen «DEG», som brukes til å skifte mellom «DEG» = grader, «RAD» = radianer og «GRAD» = gradianer, altså på hvilket format vinkelmålet oppgis.

Navngivingen i en trekant kan være vilkårlig. Vi bør derfor huske at sinus er motstående katet over hypotenus, cosinus er hosliggende katet over hypotenus og tangens er motstående katet over hosliggende katet, i stedet for å pugge formlene med a, b og c.

Oppgave 2:

I en rettvinklet trekant med navn som i figuren under har vi at vinkelen v = 42° og d = 10. Finn lengdene til c og e.

Se løsningsforslag

Inverse trigonometriske funksjoner

Vi har så langt sett hvordan vi kan beregne lengden til sidene i en rettvinklet trekant basert på størrelsen til vinkler, men vi kan også beregne vinkler basert på lengden til sidene. Har vi for eksempel formelen $\tan v = \frac{\displaystyle b}{\displaystyle a}$ og vet at b = 3 og a = 6, følger det at $\tan v = {\large \frac{3}{6}} = 0{,}5$. Nå kjenner vi ikke vinkelen og skal finne tangens, men kjenner tangens og skal finne vinkelen.

I slike tilfeller bruker vi inverse funksjoner, også kalt omvendte funksjoner. Det finnes inverse funksjoner for både sinus, cosinus og tangens, de heter asin, acos og atan alternativt arcsin, arccos og arctan. De skrives ofte også som sin⁻¹, cos⁻¹ og tan⁻¹. På bildet av Windows-kalkulatoren under har vi aktivert disse funksjonene ved å trykke på pil-opp, slik det er markert.

Har vi for eksempel at tangens er 0,5, som nevnt over, bruker vi den inverse tangensfunksjonen, og finner at tan⁻¹ 0,5 ≈ 26,6°. Den tilhørende vinkelen er altså 26,6°.

Eksempel 2:

I trekanten under er det oppgitt at sidelengdene a = 7 og c = 9 og vi skal finne vinkelen B.

Vi vet at cosinus til en vinkel er lik hosliggende katet over hypotenusen, så vi får at

$\cos B = \frac{\displaystyle a}{\displaystyle c} = {\large \frac{7}{9}} \approx 0{,}78$.

Vi får da at

B = cos⁻¹ 0,78 ≈ 38,7°.

Oppgave 3:

I trekanten i eksempel 2 vet vi at sidelengdene a = 7 og c = 9. Bruk trigonometri til å finne vinkelen A. Kontroller at vinkelsummen i trekanten blir 180°, når du fra eksempel 2 vet at vinkelen B er om lag 38,7°.

Se løsningsforslag

Trigonometri i vilkårlige trekanter

Vi har i forrige avsnitt sett hvordan vi kan beregne vinkler og sidelengder i rettvinklede trekanter. Nå skal vi se på noen regler som gjelder i vilkårlige trekanter, slik som den under.

Arealsetningen

Arealsetningen sier at arealet av en vilkårlig trekant er halve produktet av lengden til 2 sider og sinus til vinkelen mellom dem.

Med referanse til trekanten over får vi

$\fbox{$\text{Areal} = {\large \frac{1}{2}} a b \sin C = {\large \frac{1}{2}} b c \sin A = {\large \frac{1}{2}} a c \sin B$}$

Eksempel 3:

I trekanten over er sidelengden a = 9, sidelengden c = 9,8, vinkelen B = 30°, og vi skal beregne arealet. Arealsetningen gir

$\text{Areal} = {\large \frac{1}{2}} a c \sin B =  {\large \frac{1}{2}} \cdot 9 \cdot 9{,}8 \cdot \sin 30^\circ =  {\large \frac{1}{2}} \cdot 9 \cdot 9{,}8 \cdot 0{,}5 = 22{,}05$

Sinus til en rett vinkel er 1. Hvis for eksempel vinkelen C er rett, får vi fra formelen over at

$\text{Areal} = {\large \frac{1}{2}} a b \cdot 1 ={\large \frac{1}{2}} a b$

Noe som vi kjenner igjen som formelen for å beregne arealet av en rettvinklet trekant med kateter a og b. Denne formelen er altså et spesialtilfelle av arealsetningen.

Sinussetningen

Sinussetningen sier at i en vilkårlig trekant er forholdet mellom sinus til en vinkel og lengden til den motstående siden i en trekant den samme for alle de tre vinklene og sidene. Med trekanten over som eksempel har vi altså at

$\fbox{$\frac{\displaystyle \sin A}{\displaystyle a} =\frac{\displaystyle \sin B}{\displaystyle b} =\large \frac{\displaystyle \sin C}{\displaystyle c}$}$

Eksempel 4:

I trekanten over er sidelengden a = 9, sidelengden c = 9,8, vinkelen A = 66°, og vi skal beregne vinkelen C. Sinussetningen gir

$ \frac{\displaystyle \sin C}{\displaystyle c} = \frac{\displaystyle \sin A}{\displaystyle a} \Rightarrow \sin C = \frac{\displaystyle c \cdot\sin A}{\displaystyle a} =  {\large \frac{9,8 \cdot\sin 66^\circ}{9}} \approx 0{,995}$

Så C = sin⁻¹ 0,995 ≈ 84°.

Vi ser at dette er riktig, fordi vinkelsummen i en trekant skal være 180°, og

A + B + C = 66° + 30° + 84° = 180°.

Cosinussetningen

Cosinussetningen sier at i en vilkårlig trekant er kvadratet av en sidelengde lik summen av kvadratene av de andre to sidelengdene minus to ganger produktet av de to sidelengdene og cosinus til vinkelen mellom dem.

Med referanse til trekanten over, får vi at

$\fbox{$\begin{align} &a^2 = b^2 + c^2 − 2bc \cos A \\
&\\
&b^2 = a^2 + c^2 − 2ac \cos B \\
&\\
&c^2 = a^2 + b^2 − 2ab \cos C \end{align}$}$

Eksempel 5:

I trekanten over er sidelengden a = 9, sidelengden c = 9,8, vinkelen B = 30°, og vi skal beregne sidelengden b. Cosinussetningen gir

b² = a² + c² − 2ac cos B = 9² + 9,8² − 2 · 9 · 9,8 · cos 30° ≈ 24,273.

Så $b \approx \sqrt{24,273} \approx 4{,}9$.

Oppgave 4:

I trekanten under er det gitt to sidelengder, a = 7 og c = 9, samt en vinkel, B = 40°. Beregn

1. Sidelengden b.
    
2. Vinklene A og C.
    
3. Trekantens areal.

Se film med løsningsforslag 
 (Her brukes en eldre utgave av Windows-kalkulatoren)

Cosinussetningen kalles også «den utvidede pytagoreiske setning». For hvis for eksempel vinkelen C er rett, er cos C = 0, og formelen blir redusert til den vanlige pytagoreiske setningen:

c² = a² + b² − 2ab · cos C = a² + b² − 2ab · 0 = a² + b²

Trigonometriske sammenhenger

Verdiene til de trigonometriske funksjonene kan ofte bare uttrykkes som desimaltall, men for vinkler på 0, 30, 45, 60 og 90 grader blir verdiene hele tall, eller kan uttrykkes som røtter av hele tall, som vist i tabellen under:

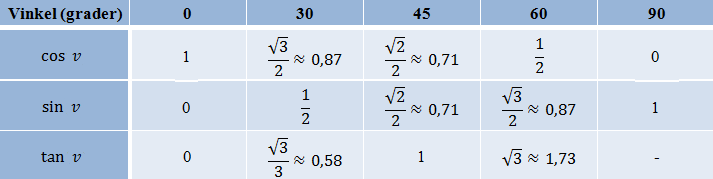
I en rettvinklet trekant som vist under, kaller vi vinklene ved hypotenusen for v og v′:

Siden vinkelsummen i en trekant er 180°, og 90° går bort i den rette vinkelen, må vi ha v′ = 90° − v.

Ved å bruke reglene for trigonometriske funksjoner i trekanter, ser vi at vi har:

$\begin{align} \sin v &= \frac{\displaystyle b}{\displaystyle c} \\
\cos v &= \frac{\displaystyle a}{\displaystyle c} \\
\sin v′ &= \frac{\displaystyle a}{\displaystyle c} \\
\cos v′ &= \frac{\displaystyle b}{\displaystyle c} \end{align}$

Sinus til v er altså lik cosinus til v′ og omvendt. Og siden v′ = 90° − v, ser vi at vi har

$\fbox{$\cos v = \sin(90^ \circ − v)$}$

$\fbox{$\sin v = \cos (90^ \circ − v)$}$

Disse sammenhengene gjelder for alle vinkler.

I trekanten over har vi også at

$\tan v = \frac{\displaystyle b}{\displaystyle a}$

Og ved å skrive om formlene for sinus og cosinus over, har vi at

b = c sin v

a = c cos v

Vi har altså at $\tan v = \frac{\displaystyle b}{\displaystyle a} = \frac{\displaystyle c \cdot \sin v}{\displaystyle c \cdot \cos v} = \frac{\displaystyle \sin v}{\displaystyle \cos v}$.

Tangens er lik sinus dividert på cosinus. Denne sammenhengen gjelder for alle vinkler.

$\fbox{$\tan v = \frac{\displaystyle \sin v}{\displaystyle \cos v}$}$

Oppgave 5:

Undersøk om sammenhengene

$\cos v = \sin(90^ \circ − v)$

$\tan v = \frac{\displaystyle \sin v}{\displaystyle \cos v}$

er riktige for vinklene 0, 30, 45, 60 og 90 grader, slik de er vist i tabellen lenger opp.

Se løsningsforslag

Kilder

• • Gulliksen, T. & Hole, A. (2010). Matematikk i praksis. Universitetsforlaget