Introduksjon
Vi skal sette inn et punkt A i (1, 2) og et punkt C i ( 4, 3) ved å skrive i inntastingsfeltet, og deretter trekke en linje mellom punktene ved å velge «Linjestykke mellom to punkt» fra verktøylinja.
Vi skriver først (1, 2), deretter C = (4, 3) i inntastingsfeltet. Så velger vi «Linjestykke mellom to punkt» og klikker på de to punktene etter tur.

Vi skal bruke GeoGebra til å tegne grafen til funksjonen f(x) = 4x3 − 48x2 + 144x, og plotte punktene på grafen som har x-verdi −1 og 1. Punktene skal hete A og B.
Vi skriver følgende i inntastingsfeltet:
funksjon(4x^3 – 48x^2 + 144x, 0, 6)
Så går vi til Innstillinger-dialogboksen og endrer akseverdiene til om lag
x-min = −2
x-maks = 8
y-min = −50
y-maks = 150
Grafen er vist under:

 Se den tilhørende GeoGebra-fila
Se den tilhørende GeoGebra-fila
Funksjonsanalyse
Vi skal ta utgangspunkt i funksjonen f(x) = x3 + 2x2 − x − 2, og bruke GeoGebra til å
-
- Finne ekstremalpunktene til funksjonen.
Vi skriver funksjonsforskriften i inntastingsfeltet: x^3 + 2x^2 – x – 2.
Ekstremalpunktene finner vi ved å skrive: ekstremalpunkt(f) i inntastingsfeltet.
GeoGebra angir at funksjonen har et maksimalpunkt i (−1,55, 0,63) og et minimalpunkt i (0,22, −2,11).
- Finne funksjonens vendepunkt.
Vi skriver: vendepunkt(f) i inntastingsfeltet.
GeoGebra angir at funksjonen har et vendepunkt i (−0,67, −0,74).
- Løse likningen x3 + 2x2 − x − 2 = 0.
Vi finner den tilhørende funksjonens nullpunkter ved å skrive: nullpunkt(f) i inntastingsfeltet.
GeoGebra angir at nullpunktene er (−2, 0), (−1, 0) og (1, 0).
Løsningen er altså x1 = −2, x2 = −1, x3 = 1.
En annen løsningsmetode kan være å finne skjæringspunktene mellom f(x) og x-aksen.
- Finne ekstremalpunktene til funksjonen.
 Se den tilhørende GeoGebra-fila
Se den tilhørende GeoGebra-fila
Vi skal finne eventuelle asymptoter til funksjonene
-
- $f(x) = 3 + \frac{\displaystyle 2}{\displaystyle x + 4}$
Vi skriver: 3 + 2 / (x + 4) i inntastingsfeltet.
Vi skriver: asymptote(f) i inntastingsfeltet.
GeoGebra viser ei liste med y = 3 og x = −4 i algebrafeltet, og tegner disse to asymptotene i grafikkfeltet.
- $g(x) = x^2 + 3x − 2$
Vi skriver: 3x^2 + 3x – 2 i inntastingsfeltet.
Vi skriver: asymptote(g) i inntastingsfeltet.
GeoGebra viser ei tom liste i algebrafeltet. Funksjonen har ingen asymptoter.
- $f(x) = 3 + \frac{\displaystyle 2}{\displaystyle x + 4}$
Vi har her forutsatt at det ikke er noen funksjoner registrert fra før, slik at navnene automatisk blir f og g.
Basert på målingene i tabellen under skal vi bruke glidere i GeoGebra til å anslå en funksjonsforskrift for en lineær funksjon, f(t), som kan brukes som modell for forsøket.
| Tid (min) | 10 | 11 | 12 | 13 | 14 |
| Temperatur (grader Celsius) | 60 | 64 | 70 | 76 | 80 |
-
- Ved å eksperimentere med glidere for a og b, finner vi at funksjonen f(t) = 5t + 10 ser rimelig bra ut. Her er det imidlertid rom for variasjon, så det kan godt være du har funnet noe som er bedre.
- f(0) = 10. Vannet holdt 10 grader da forsøket startet.
- Stigningstallet a = 5, derfor stiger temperaturen med 5 grader per minutt.
- Funksjonsforskriften kan ikke brukes til å anslå hvilken temperatur vannet vil ha etter 30 minutter. f(30) = 160, og modellen er bare gyldig opp til 100 grader.
- Ved å eksperimentere med glidere for a og b, finner vi at funksjonen f(t) = 5t + 10 ser rimelig bra ut. Her er det imidlertid rom for variasjon, så det kan godt være du har funnet noe som er bedre.
 Se den tilhørende GeoGebra-fila
Se den tilhørende GeoGebra-fila
Delt funksjonsforskrift
Vi skal bruke kommandoen Dersom i GeoGebra til å plotte funksjonen $f(x) = \begin{cases} x+2, & x < 1 \\ 2x+1, & x \ge 1 \\ \end{cases}$.
Vi kan enten bruke x < 1 som kriterium og skrive dersom(x < 1, x + 2, 2x + 1) i inntastingsfeltet, eller vi kan bruke x ≥ 1 som kriterium og skrive dersom(x >= 1, 2x + 1, x + 2).
Plottet ser i begge tilfeller slik ut:

Vi skal bruke kommandoen Dersom i GeoGebra til å plotte funksjonen $f(x) = \begin{cases} 1, & x < 1 \\ 2, & 1 \le x < 2 \\ 3, & 2 \le x \\ \end{cases}$.
Det finnes flere måter å velge kriteriene på, men vi kan for eksempel skrive dersom(x < 1, 1, 1 ≤ x < 2, 2, 3).
Plottet ser slik ut:

Derivasjon
Vi skal bruke GeoGebra til å finne første og fjerdederiverte til funksjonen f(x) = 3x5 + 2x4 − 3x3 − x2 + 2x − 1.
Vi skriver funksjonsforskriften i inntastingsfeltet: 3x^5 + 2x^4 – 3x^3 – x^2 + 2x – 1.
Vi skriver: f′(x) eller derivert(f) i inntastingsfeltet.
GeoGebra tegner grafen i grafikkfeltet og angir funksjonsforskriften i algebrafeltet: f′(x) = 15x4 +8x3 − 9x2 − 2x + 2.
Vi skriver: f′′′′(x) eller derivert(f, 4) i inntastingsfeltet.
GeoGebra tegner grafen i grafikkfeltet og angir funksjonsforskriften i algebrafeltet: f′′′′(x) = 360x + 48.
Integrasjon
Vi skal bruke GeoGebra til å beregne integralet $\int 3x^2dx$.
Vi skriver funksjonsforskriften i inntastingsfeltet: 3x^2.
GeoGebra viser funksjonsforskriften f(x) = 3x2 i algebrafeltet og grafen til f(x) i grafikkfeltet.
Vi skriver integralkommandoen i inntastingsfeltet: integral(f).
GeoGebra oppretter den integrerte funksjonen, g, viser funksjonsforskriften g(x) = x3 i algebrafeltet og grafen til g(x) i grafikkfeltet.
Hvis vi ikke har bruk for den opprinnelige funksjonen, kan vi hoppe over den, og skrive integral(3x^2).
Vi kan også åpne CAS («Vis» – «CAS») og skrive integral(3x^2) hvis vi ikke er interessert i grafen.
Trigonometri
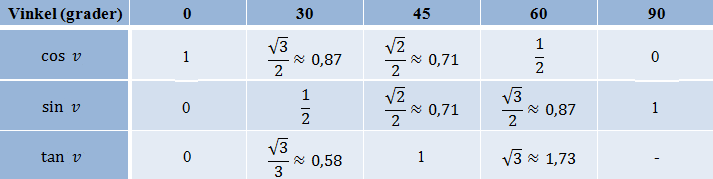
Vi skal bruke GeoGebra til å illustrere definisjonen av cosinus.
Vi bruker samme oppskrift som for illustrasjon av sinus, vist i eksempel 1. De første fire punktene blir like. Men i punkt 5 skal vi lage et linjestykke fra C som står vinkelrett på y-aksen. Dette punktet vil ha x-koordinat 0, og samme y-koordinat som C: (0, y(C)). Så vi skriver: linjestykke(C, (0, y(C))).
Vi skal bygge ut det vi laget i oppgave 1 til å tegne grafen til cosinus. Vi skal følge oppskriften på å tegne grafen til sinus, fra eksempel 2.
Vi baserer oss på de 5 trinnene i eksempel 2, men I punkt 2 skal vi bruke x-koordinaten, ikke y-koordinaten til C og skriver: x(C). Denne verdien representerer cosinus, GeoGebra kaller den g i algebrafeltet. I punkt 3 bruker vi denne verdien når vi lager et punkt som har y-koordinat lik cosinus til vinkelen og skriver: (d, g). GeoGebra kaller punktet E, og vi kan sette sporing på det på samme måte som i eksempel 2.
Vi skal plotte punktet r = 1, θ = 60° i GeoGebra. Det gjør vi ved å skrive (1; 60°) i inntastingsfeltet.
Vektorer og avbildninger
Vi skal bruke GeoGebra til å:
- sette inn vektoren $\vec a$ med startpunkt i (0, 0) og sluttpunkt i (4, 3).
Vi skriver a = (4, 3) i inntastingsfeltet. Alternativt setter vi inn fra menyen «Vektor», klikker i (0, 0) og (4, 3), endrer navnet etterpå og skjuler punktene.
GeoGebra setter inn vektoren a = [4, 3] med startpunkt i (0, 0) og sluttpunkt i (4, 0).
- sette inn vektoren $\vec b$ med startpunkt i (4, 3) og sluttpunkt i (6, −1).
Vi skriver b= vektor((4, 3), (6, -1)) i inntastingsfeltet. Alternativt bruker vi menyen «Vektor» som i forrige punkt.
GeoGebra setter inn vektoren b = [2, −4] med startpunkt i (4, 3) og sluttpunkt i (6, −1).
- beregne vektoren $\vec s = \vec a + \vec b$
Vi skriver s = a + b i inntastingsfeltet.
GeoGebra setter inn vektoren s = [6, −1] med startpunkt i (0, 0) og sluttpunkt i (6, −1).
- beregne vektoren $\vec d = \vec a − \vec b$
Vi skriver d = a – b i inntastingsfeltet.
GeoGebra setter inn vektoren d = [2, 7] med startpunkt i (0, 0) og sluttpunkt i (2, 7).
- beregne lengden $| \vec a |$
Vi skriver |a| eller lengde(a) eller abs(a) i inntastingsfeltet.
GeoGebra setter inn tallet c = 5 i algebrafeltet.
- beregne prikkproduktet $\vec a \cdot \vec b$
Vi skriver a*b i inntastingsfeltet.
GeoGebra setter inn tallet e = −4 i algebrafeltet.
Vi skal bruke GeoGebra til å lage en trekant med hjørner i (3, 2), (6, 2) og (4, 4), flytte trekanten −2 enheter i x-retning og 3 enheter i y-retning, og deretter rotere den flyttede trekanten 60 grader om punktet (0, 4).
Vi velger «Mangekant» fra menyen, klikker i (3, 2), (6, 2), (4, 4) og deretter i (3, 2) igjen. GeoGebra setter inn en trekant med hjørner i disse punktene.
Vi velger «Vektor» fra menyen og setter inn en vektor som er [−2, 3], for eksempel ved å klikke i punktene (0, 0) og (−2, 3). Vi velger så «Flytt objekt med vektor» fra menyen, klikker på trekanten, deretter på vektoren. GeoGebra lager en ny trekant med hjørner i (1, 5), (4, 5) og (2, 7).
Vi setter inn et punkt i (0, 4) ved å velge «Nytt punkt» fra menyen og klikke i (0, 4). Vi velger så «Roter objekt om punkt med fast vinkel», klikker på den nye trekanten, deretter punktet i (0, 4) og skriver 60 i dialogboksen som kommer opp.
Dynamisk geometri
Vi skal lage en vilkårlig trekant og bruke den til å illustrere sinussetningen, det vil si at forholdet mellom sinus til en vinkel i en trekant og lengden på den motstående siden er likt for alle vinkler og sider i en trekant.
Vi velger «Mangekant» og klikker ut tre punkter der trekantens hjørner skal være, så klikker vi tilbake i det første punktet. Alternativt bygger vi trekanten opp ved hjelp av linjer.
Vi velger «Vinkel» og klikker parvis på de sidene vi skal opprette en vinkel mellom, hvert par i retning mot klokka.
Vi har nå en trekant med sider a, b, c og vinkler α, β, γ. Hvilke vinkler som er motstående til hvilke sider vil variere med rekkefølgen vi satte dem inn i. I det følgende antar vi at α er motstående med a, β med b og γ med c.
Vi oppretter tre variable med hvert sitt forhold mellom sinus til vinkel og sidelengde. De kan hete hva som helst, vi kaller dem fa, fb og fc. I inntastingsfeltet skriver vi
fa = sin(α)/a
fb = sin(β)/b
fc = sin(γ)/c.
De greske bokstavene henter vi fra symbolmenyen som dukker opp til høyre for inntastingsfeltet når vi setter markøren i det.
fa, fb og fc dukker opp i algebrafeltet, alle har samme verdi.
Vi velger «Tekst», klikker der boksen skal stå og skriver inn en ledetekst, for eksempel «Forhold a: «. Så setter vi inn det tilhørende objektet, som vi har kalt fa, ved å hente det fra «Objekt»-menyen i tekstboksen. NB! Dette må hentes fra menyen, vi kan ikke bare skrive inn navnet på det. Vi gjør tilsvarende for de andre to objektene.
Nå kan vi klikke på pila til venstre i verktøylinja, ta tak i et av hjørnene i trekanten og dra. Når trekanten endrer form, endrer forholdstallene seg, men de tre er alltid like.
 Åpne GeoGebra-fil med ferdig konstruksjon
Åpne GeoGebra-fil med ferdig konstruksjon
Regresjon
Vi skal bruke regresjon i GeoGebra til å finne forskriften til en lineær funksjon som kommer så nærme punktene i lista under som mulig.
| Kvarter | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Kilometer | 22 | 38 | 58 | 80 | 104 | 122 | 138 | 161 |
Vi henter fram regnearkfeltet hvis det ikke allerede er framme: «Vis» – «Regneark».
Vi skriver inn lista med målinger i regnearket, kvarter i kolonne A og kilometer i kolonne B.
Vi markerer tallene, høyreklikker og velger «Lag» – «Liste med punkt».
GeoGebra lager ei liste som heter Liste1.
Vi skriver: reglin(Liste1) i inntastingsfeltet.
GeoGebra foreslår funksjonsforskriften y = 20,11x − 0,11 i algebrafeltet og tegner den tilhørende grafen i grafikkfeltet.
Matematisk er nok denne nøyaktig, men vi ser at det ikke representerer situasjonen helt godt. Den sier at når turen starter har familien kjørt 0,11 kilometer feil vei.
 Se den tilhørende GeoGebra-fila
Se den tilhørende GeoGebra-fila
Vi skal bruk funksjonen regpot i GeoGebra til å finne en potensfunksjon som beskriver situasjonen i tabellen under.
| Tid (sekunder) | 1 | 2 | 3 | 4 | 5 |
| Distanse (meter) | 4,9 | 19,6 | 44,1 | 78,4 | 122,5 |
Vi henter fram regnearkfeltet hvis det ikke allerede er framme: «Vis» – «Regneark».
Vi skriver inn lista med målinger i regnearket, tid i kolonne A og distanse i kolonne B.
Vi markerer tallene, høyreklikker og velger «Lag» – «Liste med punkt».
GeoGebra lager ei liste som heter Liste1.
Vi skriver: regpot(Liste1) i inntastingsfeltet.
GeoGebra foreslår funksjonsforskriften f(x) = 4,9x2 i algebrafeltet og tegner den tilhørende grafen i grafikkfeltet.
Funksjonsforskriften er helt korrekt, formelen for fritt fall er $d = {\large \frac{1}{2}}gt^2$, der d er falt distanse, t er tida og g er tyngdens akselerasjon som er om lag 9,8.
 Se den tilhørende GeoGebra-fila
Se den tilhørende GeoGebra-fila
Statistikk
Vi skal bruke GeoGebra til å lage et søylediagram som viser fordeling av følgende karakterer:1, 4, 5, 5, 4, 1, 3, 4, 2, 2, 2, 4, 4, 4, 3, 3, 1, 3, 2, 5, 6, 3, 1, 4, 2. Søylebredden skal være 0,75.
Metode 1:
Vi skriver tallene inn i et celleområde i regnearket i GeoGebra, for eksempel A1:E5. I inntastingsfeltet skriver vi så søylediagram(A1:E5, 0.75). GeoGebra lager søylediagrammet under:

Metode 2:
Karakterene fordeler seg slik:
| Karakter | 1 | 2 | 3 | 4 | 5 | 6 |
| Frekvens | 4 | 5 | 5 | 7 | 3 | 1 |
Vi skriver karakterene i én kolonne i regnearket i GeoGebra, for eksempel A1:A6 og frekvensen i en annen, for eksempel B1:B6. I inntastingsfeltet skriver vi så søylediagram(A1:A6, B1:B6, 0.75). GeoGebra lager samme søylediagram som ved metode 1.
Vi skal bruke GeoGebra til å lage et histogram som viser fordeling av karakterene fra oppgave 1, med intervaller 1-2, 3, 4 og 5-6.
Karakterene er fordelt slik:
| Karakter | 1 – 2 | 3 | 4 | 5 – 6 |
| Frekvens | 9 | 5 | 7 | 4 |
Det er sagt at intervallgrensene skal være 0,5-2,5, 2,5-3,5, 3,5-4,5 og 4,5-6,5. Så vi skriver 0.5, 2,5, 3.5, 4.5, 6.5 i én kolonne, for eksempel i cellene A1 – A5. Frekvensen, altså 9, 5, 7, 4 skriver vi en annen kolonne, for eksempel i cellene B1 – B4. Intervallbredden beregner vi så for hvert intervall. Vi skriver = A2 – A1 for eksempel i celle C1, tar tak i hjørnet og drar ned til C4. Til slutt beregner vi søylehøyden for hvert intervall. Vi skriver = B1 / C1 for eksempel i celle D1, tar tak i hjørnet og drar ned til D4.
I inntastingsfeltet skriver vi så histogram(A1:A5, D1:D4). GeoGebra lager histogrammet under:

Vi skal lage et boksplott av dataene 6, 25, 15, 8, 29, 14, 27, 30, 0, 29, 0, 2, 23, 125, 5, 30, 20, 10, 14, sentrert rundt y = 1 og med total bredde 1.
-
- Basert på rådataene.
Vi skriver boksplott(1, 0.5,{6, 25, 15, 8, 29, 14, 27, 30, 0, 29, 0, 2, 23, 125, 5, 30, 20, 10, 14}), eller legger inn dataene i regneark-delen. Legger vi dataene i celle A1 – A19, skriver vi etterpå boksplott(1, 0.5, A1:A19).
- Basert på at laveste verdi er 0, første kvartil 6, median 15, tredje kvartil 29 og største verdi 125.
Vi skriver boksplott(1, 0.5, 0, 6, 15, 29,125).
- Basert på rådataene.
I begge tilfeller lager GeoGebra boksplottet under:

X betegner antall kron i 8 kast med en juksemynt der sannsynligheten for kron er 0,6, og vi skal bruke sannsynlighetskalkulatoren i GeoGebra til beregninger.
Hvis den ikke alt er framme, tar vi opp sannsynlighetskalkulatoren ved å klikke på «Vis» – «Sannsynlighetskalkulator».
Vi velger «Binomisk fordeling» og setter «n» = 8 og «p» = 0,6.
Vi skal så beregne
-
- Fordelingens forventningsverdi og standardavvik.
Vi leser av at forventningen er μ = 4,8 og standardavviket er σ ≈ 1,3856.
- P(X = 4)
Vi velger «Intervall», og setter 4 både som øvre og nedre grense. Alternativt drar vi begge pilene inn under kolonne 4. GeoGebra svarer 0,2322. Dette er illustrert under:

- P(X ≤ 2)
Vi velger «Venstresidig», og setter 2 som øvre grense. Alternativt drar vi pila inn under kolonne 2. GeoGebra svarer 0,0498.
- P(X > 6)
I en diskret fordeling har vi at P(X > x) = (X ≥ x + 1).
Så P(X > 6) = P(X ≥ 7).
Vi velger «Høyresidig», og setter 7 som nedre grense. Alternativt drar vi pila inn under kolonne 7. GeoGebra svarer 0,1064.
- Fordelingens forventningsverdi og standardavvik.
I en forening med 65 medlemmer er 13 negative til et forslag, og vi skal bruke sannsynlighetskalkulatoren i GeoGebra til beregninger.
Hvis den ikke alt er framme, tar vi opp sannsynlighetskalkulatoren ved å klikke på «Vis» – «Sannsynlighetskalkulator».
Vi velger «Hypergeometrisk fordeling» og setter «populasjon» = 65, «n» = 13 og «utvalg» = 20.
Vi skal finne fordelingens forventning og standardavvik, noe vi leser av til å være μ = 4 og σ ≈ 1,5.
Så skal vi finne sannsynligheten for at
-
- Ingen av representantene er negative.
Vi velger «Intervall», og setter 0 både som øvre og nedre grense. Alternativt drar vi begge pilene inn under kolonne 0. GeoGebra svarer 0,0044.
- Én av representantene er negativ.
Vi velger «Intervall», og setter 1 både som øvre og nedre grense. Alternativt drar vi begge pilene inn under kolonne 1. GeoGebra svarer 0,035.
- To eller flere av representantene er negative.
Vi velger «Høyresidig», og setter 2 som nedre grense. Alternativt drar vi pila inn under kolonne 2. GeoGebra svarer 0,9605.
- Ingen av representantene er negative.
I en vannprøve er det i gjennomsnitt to hoppekreps. Vi antar at mengden hoppekreps er poissonfordelt, og skal bruk sannsynlighetskalkulatoren i GeoGebra til beregninger.
Hvis den ikke alt er framme, tar vi opp sannsynlighetskalkulatoren ved å klikke på «Vis» – «Sannsynlighetskalkulator».
Vi velger «Poissonfordeling» og setter «μ» = 2.
Så skal vi finne sannsynligheten for at en annen, like stor vannprøve inneholder
- Ingen hoppekreps.
Vi velger «Intervall», og setter 0 både som øvre og nedre grense. Alternativt drar vi begge pilene inn under kolonne 0. GeoGebra svarer 0,1353
- Én hoppekreps.
Vi velger «Intervall», og setter 1 både som øvre og nedre grense. Alternativt drar vi begge pilene inn under kolonne 1. GeoGebra svarer 0,2707.
- To eller flere hoppkreps.
Vi velger «Høyresidig», og setter 2 som nedre grense. Alternativt drar vi pila inn under kolonne 2. GeoGebra svarer 0,594.
På en eksamen er resultatene normalfordelt, N(14, 22). Laveste poengsum for å stå er 12 poeng, og vis skal bruke sannsynlighetskalkulatoren i GeoGebra til å beregne hvor stor del av de som tar eksamenen som kan forventes å stryke.
Hvis den ikke alt er framme, tar vi opp sannsynlighetskalkulatoren ved å klikke på «Vis» – «Sannsynlighetskalkulator».
Vi velger «Normalfordeling» og setter «μ» = 14 og «σ» = 2.
Vi velger «Venstresidig», og setter 12 som øvre grense. Alternativt drar vi pila inn under kolonne 12. GeoGebra svarer 0,1587.
Vi skal bruke sannsynlighetskalkulatoren i GeoGebra til å beregne et 99 % konfidensintervall for dagsproduksjonen av støtfangere, basert på at gjennomsnittet målt over seks dager er X = 217 enheter og at standardavviket til produksjonen er σ = 5,8.
Hvis sannsynlighetskalkulatoren ikke allerede er framme, velger vi «Vis» – «Sannsynlighetskalkulator», og klikker på fanen «Statistikk».
Her er vi i en målemodell med kjent standardavvik, så vi velger «Z-estimat av et gjennomsnitt» og fyller ut som vist under:

Vi ser at GeoGebra beregner konfidensintervallet til [210,9008, 223,0992]. Dette regnet vi ut for hånd i oppgave 4 om estimering.
Vi skal bruke sannsynlighetskalkulatoren i GeoGebra til å beregne et 90 % konfidensintervall for dagsproduksjonen av støtfangere, basert på at gjennomsnittet målt over seks dager X = 217 enheter og at utvalgsstandardavviket er beregnet til S = 6.
Hvis sannsynlighetskalkulatoren ikke allerede er framme, velger vi «Vis» – «Sannsynlighetskalkulator», og klikker på fanen «Statistikk».
Her er vi i en målemodell med ukjent standardavvik, så vi velger «T-estimat av et gjennomsnitt» og fyller ut som vist under:

Vi ser at GeoGebra beregner konfidensintervallet til [212,0642, 221,9358].
Vi skal bruke sannsynlighetskalkulatoren i GeoGebra til å beregne et 95 % konfidensintervall for sannsynligheten for at en vilkårlig mobillader er defekt, når det blant 2000 stikkprøver ble funnet 35 defekte.
Hvis sannsynlighetskalkulatoren ikke allerede er framme, velger vi «Vis» – «Sannsynlighetskalkulator», og klikker på fanen «Statistikk».
Her er vi i en binomisk modell, så vi velger «Z-estimat av en andel» og fyller ut som vist under:

Vi ser at GeoGebra beregner konfidensintervallet til [0,0118, 0,0232]. Dette regnet vi ut for hånd i oppgave 9 om estimering.
Vi skal bruke sannsynlighetskalkulatoren i GeoGebra til å gjøre en hypotesetest på 5 % signifikansnivå på om henholdsvis 20 av 100 og 200 av 1000 seksere ved terningkast tyder på at terningen gir for mange seksere.
Hvis sannsynlighetskalkulatoren ikke allerede er framme, velger vi «Vis» – «Sannsynlighetskalkulator», og klikker på fanen «Statistikk».
Her er vi i en binomisk modell, så vi velger «Z-test av en andel» og fyller ut som vist under:

Vi ser at GeoGebra beregner testobservatoren til Z = 0,8935. Med et lite avvik, som antakelig skyldes avrundingsfeil, regnet dette vi ut for hånd i oppgave 1 om hypotesetesting.
P-verdien på 0,1858 er ikke mindre enn signifikansnivået på 0,05, så nullhypotesen kan ikke forkastes.
Vi endrer deretter «Treff» til 200 og «N» til 1000:

GeoGebra beregner testobservatoren til Z = 2,8254. Dette regnet vi ut for hånd i oppgave 2 om hypotesetesting.
P-verdien på 0,0024 er nå mindre enn signifikansnivået på 0,05, så nullhypotesen kan forkastes.
Vi skal bruke sannsynlighetskalkulatoren i GeoGebra til å gjøre en hypotesetest på 5 % signifikansnivå på om angitt gjennomsnittlig ventetid på 30 sekunder på en telefontjeneste er satt for lavt når 15 oppringninger gir en gjennomsnittlig ventetid på 37 sekunder, med et standardavvik på 14.
Hvis sannsynlighetskalkulatoren ikke allerede er framme, velger vi «Vis» – «Sannsynlighetskalkulator», og klikker på fanen «Statistikk».
Her er vi i en målemodell med ukjent standardavvik, så vi velger «T-test av et gjennomsnitt» og fyller ut som vist under:

Vi ser at GeoGebra beregner testobservatoren til t = 1,9365.
P-verdien på 0,0366 er mindre enn signifikansnivået på 0,05, så nullhypotesen kan forkastes.
Vi skal bruke sannsynlighetskalkulatoren i GeoGebra til å gjøre en hypotesetest på 5 % signifikansnivå på om det er forskjell på mengden sukker to maskiner tilsetter en matvare. 60 stikkprøver av maskin X gir et snitt på 10,107 gram sukker, og 75 stikkprøver av maskin Y gir et snitt på 10,061 gram sukker. Standardavvikene er kjent som, 0,11 gram for maskin X og 0,13 gram for maskin Y.
Hvis sannsynlighetskalkulatoren ikke allerede er framme, velger vi «Vis» – «Sannsynlighetskalkulator», og klikker på fanen «Statistikk».
Her er vi i en målemodell med kjent standardavvik, så vi velger «Z-test. Forskjell mellom gjennomsnitt» og fyller ut som vist under:

Vi ser at GeoGebra beregner testobservatoren til Z = 2,2261. Dette regnet vi ut for hånd i oppgave 2 om å sammenlikne datasett.
P-verdien på 0,026 er mindre enn signifikansnivået på 0,05, så nullhypotesen kan forkastes.
Vi skal bruke sannsynlighetskalkulatoren i GeoGebra til å gjøre en hypotesetest på 5 % signifikansnivå på om det er forskjell på antall defekte sømmer på bukser produsert ved to produksjonslinjer når det ved første produksjonslinje er 147 av 2500 defekter og ved andre 151 av 2000.
Hvis sannsynlighetskalkulatoren ikke allerede er framme, velger vi «Vis» – «Sannsynlighetskalkulator», og klikker på fanen «Statistikk».
Her er vi i en binomisk modell, så vi velger «Z-test. Forskjell mellom andeler» og fyller ut som vist under:

Vi ser at GeoGebra beregner testobservatoren til Z = −2,2386. Dette regnet vi ut for hånd i oppgave 5 om å sammenlikne datasett.
P-verdien på 0,0252 er mindre enn signifikansnivået på 0,05, så nullhypotesen kan forkastes.
CAS
Vi skal bruke CAS i GeoGebra til å forenkle uttrykkene
-
- $4xy + 8z − 3xy + 5x − 3z$
- $5m^2 − 3n − 3(m^2 + n) − (−m^2 − n)$
- $\frac{\displaystyle {(a^{\large 2})}^{\large 3}a^{\large 4}}{\displaystyle {(a^{\large 3})}^{\large 2}}$
- $x^2y^2x + x^3y^3x^{−1} − x^3y^2 + x \, y \, y \, y \, y \, y^{−1}x$
- $4xy + 8z − 3xy + 5x − 3z$
Vi åpner CAS hvis det ikke allerede er åpent, og skriver
-
- 4xy + 8z – 3xy + 5x – 3z. GeoGebra forenkler uttrykket til xy + 5x + 5z.
- 5m^2 – 3n – 3(m^2 + n) – (-m^2 – n). GeoGebra forenkler uttrykket til 3m2 −5n.
- (a^2)^3 a^4 / (a^3)^2. GeoGebra forenkler uttrykket til a4.
- x^2y^2x + x^3y^3x^-1 – x^3y^2 + x*y*y*y*y*y^-1x. GeoGebra forenkler uttrykket til 2x2y3.
- 4xy + 8z – 3xy + 5x – 3z. GeoGebra forenkler uttrykket til xy + 5x + 5z.
Vi skal bruke CAS til å forenkle uttrykkene
-
- $\sqrt[\Large 3]{x^4} \cdot \sqrt[\Large 3]{x^{\phantom 1}}$
- $\frac{\displaystyle \sqrt{a^\phantom 1} \cdot \sqrt[\Large 4]{a^3} \cdot a}{\displaystyle \sqrt[\Large 8]{a^5} }$
- $\sqrt[\Large 3]{x^4} \cdot \sqrt[\Large 3]{x^{\phantom 1}}$
Vi åpner CAS hvis det ikke allerede er åpent, og skriver
-
- nrot(x^4, 3) nrot(x, 3). GeoGebra svarer imidlertid bare med $\sqrt[\Large 3]{x^{\phantom 1}}\sqrt[\Large 3]{x^4}$.
Vi bruker derfor kommandoen forenkle, og skriver
forenkle(nrot(x^4, 3) nrot(x, 3)). GeoGebra forenkler nå uttrykket til $x \sqrt[\Large 3]{x^2}$.
- forenkle(sqrt(a) nrot(a^3, 4) a / nrot( a^5, 8)). GeoGebra forenkler uttrykket til $a \sqrt[\Large 8]{a^5}$.
- nrot(x^4, 3) nrot(x, 3). GeoGebra svarer imidlertid bare med $\sqrt[\Large 3]{x^{\phantom 1}}\sqrt[\Large 3]{x^4}$.
Vi skal bruke CAS til å regne ut (x + 5)3.
Vi åpner CAS hvis det ikke allerede er åpent, og skriver inn regnut((x + 5)^3). GeoGebra svarer x3 + 15x2 + 75x + 125.
Vi skal bruke CAS til å løse likningssettet:
(I) x + 3y − 2z = 5
(II) 3x + 5y + 6z = 7
(III) 2x + 4y + 3z = 8
Vi åpner CAS og legger inn likningene, én i hver rute. Deretter markerer vi alle likningene ved å klikke på rute «1», holde nede <skift> og klikke på rute «3». Så klikker vi på «Løs» eller «Nøs Numerisk». Siden løsningene er hele tall, spiller det i dette tilfellet ikke noen rolle hva vi velger. GeoGebra viser løsningen x = −15, y = 8, z = 2.
Alternativt skriver vi løs({ x + 3y – 2z = 5, 3x + 5y + 6z = 7, 2x + 4y + 3z = 8}, {x, y, z}) i CAS. Vi kan også skrive nløs i stedet for løs.
Dynamiske ark
Basert på ei GeoGebra-fil om derivasjon skal vi lage dynamiske ark.
Vi velger «Fil» – «Eksporter» – «Dynamisk ark som webside …».
Vi velger fanen «Eksporter som webside».
Vi skriver: «Derivasjon 1» i feltet «Tittel».
Vi klikker på «Eksporter».
Vi velger hva eksportfila skal ligge, for eksempel på «C:\Temp», og skriver derivasjon_1 i «Filnavn».
Basert på dynamiske fila vi laget i oppgave 1 skal vi eksperimentere med hva vi kan gjøre av endringer.
Vi kan skyve på punktet A, men ikke skru av eller på sporing eller gjøre andre endringer.
-
- Vi skal gjenta det vi gjorde i oppgave 1, men tillate høyreklikking.
Vi bruker samme metode som i oppgave 1, men etter at vi har valgt «Eksporter som webside» og før vi klikker «Eksporter», klikker vi på fanen «Avansert» og huker av for «Tillat høyreklikking, zooming og tastaturredigering».
- Vi skal gjenta det vi gjorde i oppgave 1, men nå skal også meny- og verktøylinjer er tilgjengelige.
Vi gjør det samme som i punkt 1, men vi huker nå også av for «Vis menylinje» og «Vis verktøylinje».
- Vi skal gjenta det vi gjorde i oppgave 1, men tillate høyreklikking.



 Åpne et regneark med beregningene fra oppgave 3
Åpne et regneark med beregningene fra oppgave 3