Stikkord: delmengde

Delmengder

I artikkelen om begreper i sannsynlighet ble vi kjent med begrepet mengder, og så hvordan vi kunne illustrere mengder ved hjelp av Venn-diagrammer. Vi lærte også om delmengder, der en mengde er en del av en annen, noe vi i Venn-diagrammer kan illustrere med en sirkel inni en annen sirkel.

Slike delmengder er egentlig uordnede utvalg av elementer i mengden, som vi studerte i artikkelen om ordnede og uordnede utvalg. For eksempel er hver mulig vinnerrekke i Lotto en delmengde med 7 tall i en hovedmengde på totalt 34.

Nå skal vi finne ut hvor mange delmengder det går an å lage i en mengde. Diagrammene under viser en mengde med tre elementer, nemlig tallene 1, 2 og 3, og hvordan disse tallene kan organiseres i delmengder.

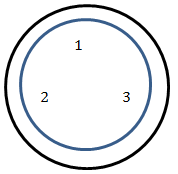Vi ser at vi kan lage 3 delmengder med ett tall i hver, 3 med to tall i hver, og 1 med alle tallene. Totalt blir dette 3 + 3 + 1 = 7 delmengder. Tenker vi oss at mengden med 0 elementer, ∅, også er en delmengde, blir det totalt 8 mulige delmengder.

Det er lett å se for seg at en mengde med to elementer vil kunne inneholde 4 delmengder, nemlig 2 med ett element, 1 med to elementer og 1 med 0 elementer. En mengde med ett element vil kunne inneholde 2 delmengder, nemlig 1 med ett element og 1 med ingen elementer. En mengde med 0 elementer vil bare kunne inneholde 1 delmengde, nemlig mengden med 0 elementer.

I alle tilfeller blir antall delmengder lik 2ⁿ, der n er antall elementer. 2⁰ = 1, 2¹ = 2, 2² = 4, 2³ = 8. Grunnen til at det er slik, er at det for hvert element finnes to muligheter: Elementet kan være med i en delmengde eller ikke. Har vi en mengde med m delmengder og introduserer et nytt element, vil vi kunne lage m nye delmengder som inkluderer det nye elementet, og får doblet antall mulige delmengder.

$\fbox{En mengde med $n$ elementer kan inneholde $2^n$ delmengder}$

Oppgave 1:

En mengde, A, inneholder elementene a, b og c: A = {a, b, c}. List opp de mulige delmengdene som kan lages. Stemmer dette antallet med det som er angitt i boksen over?

Se løsningsforslag

At en mengde, B, er en delmengde av A, skriver vi slik: $B \subseteq A$.

At en mengde, B, ikke er en delmengde av A, skriver vi slik: $B \nsubseteq A$.

Vi har sett at en delmengde kan bestå av alle elementene i en mengde, en mengde er altså en delmengde av seg selv. Men bare delmengder som ikke er lik mengden selv kalles ekte delmengder.

At en mengde, B, er en ekte delmengde av A, skriver vi slik: $B \subset A$.

At en mengde, B, ikke er en ekte delmengde av A, skriver vi slik: $B \not \subset A$.

Eksempel 1:

$\{2, 3 \} \subseteq \{2, 3, 4 \}$

$\{2, 3 \} \subset \{2, 3, 4 \}$

$\{2, 3, 4 \} \subseteq \{2, 3, 4 \}$

$\{2, 3, 4 \} \not\subset \{2, 3, 4 \}$

$\emptyset \subseteq \{2, 3, 4 \}$

$\emptyset \subset \{2, 3, 4 \}$

$\{1 \} \nsubseteq \{2, 3, 4 \}$

$\{2, 3, 4, 5 \} \nsubseteq \{2, 3, 4 \}$

Eksempel 2:

Vi skal sjekke hvor mange delmengder med henholdsvis 1, 2 og 3 elementer som kan lages i en mengde med totalt 3 elementer. Som nevnt er en delmengde det samme som et uordnet utvalg, så vi bruker formelen for antall uordnede utvalg:

0 elementer: ${\large \binom{3}{0}} = {\large \frac{3!}{0!(3 − 0)!}} = 1$.

1 element: ${\large \binom{3}{1}} = {\large \frac{3!}{1!(3 − 1)!}} = 3$.

2 elementer: ${\large \binom{3}{2}} = {\large \frac{3!}{2!(3 − 2)!}} = 3$.

3 elementer: ${\large \binom{3}{3}} = {\large \frac{3!}{3!(3 − 3)!}} = 1$.

Dette stemmer med det vi har funnet tidligere. Og totalt blir det 1 + 3 + 3 + 1 = 8, som er 2³, som det skal være.

Se filmen «Delmengder»