I artikkelen om kontinuitet og grenser ser vi på grenser som en funksjonsverdi nærmer seg når variabelen nærmer seg en gitt verdi, eller når den nærmer seg pluss/minus uendelig.
I brøker kan vi imidlertid oppleve at det ikke er opplagt om et funksjonsuttrykk har en grenseverdi, og i så fall hva den er, fordi vi får et ubestemt uttrykk, der både teller og nevner går mot 0 eller uendelig samtidig.
Eksempel 1:
$\displaystyle \lim_{x \to \infty} \frac{\displaystyle x^3 + 6x}{\displaystyle 3x^3 + x^2 + 1} = \frac{\infty}{\infty}$
Dividere med høyeste potens
I artikkelen om asymptoter ser vi hvordan vi kan løse problemet med ubestemte uttrykk i rasjonale funksjoner ved å dividere alle ledd i teller og nevner med høyeste potens av variabelen, slik som i eksempel 2, under:
Eksempel 2:
$\displaystyle \lim_{x \to \infty} \frac{\displaystyle x^3 + 6x}{\displaystyle 3x^3 + x^2 + 1} = \displaystyle \lim_{x \to \infty} \frac{\displaystyle \frac{x^3}{x^3} + \frac{6x}{x^3}}{\displaystyle \frac{3x^3}{x^3} + \frac{x^2}{x^3} + \frac{1}{x^3}} =\displaystyle \lim_{x \to \infty} \frac{\displaystyle 1 + \frac{6}{x^2}}{\displaystyle 3 + \frac{1}{x} + \frac{1}{x^3}} = \frac{\displaystyle 1 +0}{\displaystyle 3 + 0 + 0} = \frac{1}{3}$
Har vi et brøkuttrykk som ikke er en rasjonal funksjon, trenger imidlertid ikke metoden med å dividere med høyeste potens av variabelen å føre fram, slik som i eksempel 3, under:
Eksempel 3:
$\displaystyle \lim_{x \to \infty} \frac{\displaystyle 5x}{\displaystyle e^x} = \frac{\infty}{\infty}$
Her hjelper det ikke å dividere teller og nevner med x, da får vi en delbrøk som er $\frac{\displaystyle e^x}{\displaystyle x}$, og vi er like langt.
L′Hôpitals regel
I alle uttrykk som går mot ${\large \frac{0}{0}}$ eller ${\large \frac{\pm \infty}{\pm \infty}}$, kan vi imidlertid løse opp i floken ved å benytte noe som heter l′Hôpitals regel, oppkalt etter den franske matematikeren Guillaume François Antoine, marquis de l′Hôpital.
L’Hôpitals regel sier at grenseverdien i en brøk som går mot ${\large \frac{0}{0}}$ eller ${\large \frac{\pm \infty}{\pm \infty}}$, ikke endrer seg hvis vi deriverer teller og nevner hver for seg.
Eksempel 4:
Vi skal finne
$\displaystyle \lim_{x \to \infty} \frac{\displaystyle 5x}{\displaystyle e^x}$
som i eksempel 3.
Her har vi et uttrykk som er ${\large \frac{\infty}{\infty}}$, og kan bruke l′Hôpitals regel. Deriverer vi telleren, får vi (5x)’ = 5, og deriverer vi nevneren, får vi (ex)’ = ex.
Når x → ∞, vil ex → ∞, så vi får:
$\displaystyle \lim_{x \to \infty} \frac{\displaystyle 5x}{\displaystyle e^x} = \lim_{x \to \infty} \frac{\displaystyle (5x)’}{\displaystyle (e^x)’} = \lim_{x \to \infty} \frac{\displaystyle 5}{\displaystyle e^x} = \frac{\displaystyle 5}{\displaystyle \infty} = 0$
NB! I l′Hôpitals regel bruker vi ikke kvotientregelen, men deriverer funksjonene i teller og nevner hver for seg.
Eksempel 5:
Vi skal finne
$\displaystyle \lim_{x \to 0}\frac{\sin x}{x}$
Når x → 0, vil både sin x → 0 og x → 0, så vi får en brøk med 0 i både teller og nevner:
$\displaystyle \lim_{x \to 0}\frac{\sin x}{x} = \frac{0}{0}$
Bruker vi l′Hôpitals regel, får vi:
$\displaystyle \lim_{x \to 0}\frac{\sin x}{x} = \displaystyle \lim_{x \to 0}\frac{(\sin x)’}{x’} \displaystyle \lim_{x \to 0}\frac{\cos x}{1} = \frac{1}{1} = 1$
Bruk l′Hôpitals regel til å beregne $\displaystyle \lim_{x \to 0} \frac{\displaystyle e^x − 1}{\displaystyle \sin x}$
Formelt sett uttrykker vi L′Hôpitals regel slik:
$\fbox{$\begin{align} &\text{Hvis } \displaystyle \lim_{x \to a} f(x) = \displaystyle \lim_{x \to a} g(x) = 0\\
&\text{eller } \displaystyle \lim_{x \to a} f(x) = \pm \displaystyle \lim_{x \to a} g(x) = \pm \infty \\
&\text{har vi at} \\
&\displaystyle \lim_{x \to a}\frac{\displaystyle f(x)}{\displaystyle g(x)} = \displaystyle \lim_{x \to a}\frac{\displaystyle f′(x)}{\displaystyle g′(x)}
\end{align}$}$
Gjentatt bruk av l′Hôpitals regel
Av og til må vi bruke l′Hôpitals regel flere ganger før vi får et uttrykk som ikke der ikke både teller og nevner går mot 0 eller uendelig samtidig.
Eksempel 5:
Vi bruker l′Hôpitals regel på brøken i eksempel 1.
$\displaystyle \lim_{x \to \infty} \frac{\displaystyle x^3 + 6x}{\displaystyle 3x^3 + x^2 + 1} = \displaystyle \lim_{x \to \infty} \frac{\displaystyle 3x^2 + 6}{\displaystyle 9x^2 + 2x} = \displaystyle \lim_{x \to \infty} \frac{\displaystyle 6x}{\displaystyle 18x + 2} = \frac{\displaystyle 6}{\displaystyle 18} = \frac{\displaystyle 1}{\displaystyle 3}$
Bruk l′Hôpitals regel til å beregne $\displaystyle \lim_{x \to 0} \frac{\displaystyle 1 − \cos x}{\displaystyle x^2} $
I artikkelen om asymptoter sier vi at når variabelen går mot uendelig, går en brøk med polynomfunksjoner i teller og nevner mot en konstant hvis funksjonene i teller og nevner har samme grad, mot uendelig hvis funksjonen i teller har høyere grad enn nevner, og mot 0 hvis funksjonen i teller har lavere grad enn nevner.
Hvis vi tenker oss at vi bruker l′Hôpitals regel gjentatte ganger på en slik brøk, forstår vi hvorfor det er slik. For hver derivasjon reduseres polynomenes grad med 1. Er de i utgangspunktet av samme grad, vil begge bli redusert til en konstant samtidig. Er de av forskjellig grad, vil polynomet av høyest grad fremdeles være en funksjon av x, som går mot uendelig, idet den andre funksjonen er redusert til en konstant.
Feil bruk av l′Hôpitals regel
Vi kan bare bruke l′Hôpitals regel på uttrykk som går mot ${\large \frac{0}{0}}$ eller ${\large \frac{\pm \infty}{\pm \infty}}$.
Eksempel 6:
Vi har $\displaystyle \lim_{x \to 2} \frac{\displaystyle x−2}{\displaystyle 4x} = \frac{ 0}{8} = 0$
Bruker vi l′Hôpitals regel på denne brøken, får vi
$\displaystyle \lim_{x \to 2} \frac{\displaystyle (x−2)’}{\displaystyle (4x)’} = \frac{\displaystyle 1}{\displaystyle 4}$
som er feil. Grenseverdien for brøken er verken ${\large \frac{0}{0}}$ eller ${\large \frac{\pm \infty}{\pm \infty}}$, så det er feil å bruke l′Hôpitals regel i dette tilfellet.
Vi må også passe på å ikke tolke for mye inn i l′Hôpitals regel. L′Hôpitals regel angir hva en grenseverdi er, men sier ikke noe om formen på funksjonen.
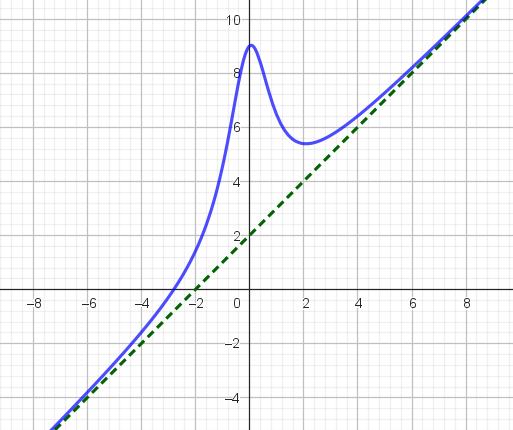
Eksempel 7:
I eksempel 9 i artikkelen om asymptoter bruker vi polynomdivisjon til å omforme brøken
$f(x) = \frac{\displaystyle x^3 + 2}{\displaystyle x^2 + 1}$
til
$f(x) = x + \frac{\displaystyle −x + 2}{\displaystyle x^2 + 1}$
Siden brøken vil gå mot 0 når x går mot uendelig, får vi at $\displaystyle \lim_{x \to \infty} f(x) = x$.
Vi konkluderer derfor med at f(x) → ∞ når x → ∞, og at linja y = x er en skråasymptote for f(x).
Det opprinnelige funksjonsuttrykket går mot uendelig på uendelig, så vi kan også bruke l′Hôpitals regel på det:
$\displaystyle \lim_{x \to \infty} f(x) = \lim_{x \to \infty} \frac{\displaystyle x^3 + 2}{\displaystyle x^2 + 1} =\lim_{x \to \infty} \frac{\displaystyle 3x^2}{\displaystyle 2x} = \lim_{x \to \infty} \frac{\displaystyle 6x}{\displaystyle 2} = 3x$
Ut fra dette kan vi lese at f(x) → ∞ når x → ∞, som vi fant da vi brukte polynomdivisjon. Men vi har skapt et nytt funksjonsuttrykk, og vi kan ikke ut av dette tolke at y = 3x er en skråasymptote for f(x).
Kilder
-
- Gulliksen, T. & Hole, A. (2010). Matematikk i praksis. Universitetsforlaget
- Thomas, G.B., Finney R.L. (1988). Calculus and Analytic Geometry. Addison-Wesley.
- matematikk.org
 Se film med løsningsforslag
Se film med løsningsforslag