Hva er en vektor?
Enkelt sagt er vektorer linjestykker med retning. Retningen angis gjerne ved piler, slik som illustrert under.

For å motivere bruken av vektorer kan vi tenke oss en mann som prøver å flytte en stein ved å dra i et tau:

Hvordan steinen vil bevege seg, avhenger både av hvilken retning mannen drar, og med hvilken kraft han drar. Vektorer er supre til å illustrere slike situasjoner. Vi lar retningen vektoren peker i symbolisere retningen mannen drar i, og lengden på vektoren symbolisere kraften han drar med.
![]()  |
 |
 |
| Drar på skrå opp |
Drar mot høyre |
Drar kraftigere mot høyre |
Vektorer tegner vi gjerne inn i et koordinatsystem, som vist under.

Vi kan navngi en vektor ved å angi endepunktene med en pil over. For eksempel vektorene $\vec{AB}$, $\vec{CD}$ og $\vec{EF}$ som er vist over. Vi kan også gi vektorene et eget navn, gjerne med liten bokstav, for eksempel $\vec{a}$, $\vec{b}$ og $\vec{c}$. Noen bøker bruker vektornavn uten pil, men med fet skrift, for eksempel a, b og c. Her kommer vi imidlertid til å konsekvent markere at noe er en vektor ved å sette pil over navnet.
En vektor har koordinater som beskriver hvordan vi forflytter oss når vi beveger oss langs vektoren. Så lenge vi holder oss i planet, vil en slik forflytning skje i x– og/eller y-retning.
Vi holder oss her til å studere vektorer i planet, men prinsippene kan enkelt utvides til å gjelde i flere dimensjoner.
Vektorkoordinater
Koordinatene til en vektor finner vi ved å ta sluttpunktets koordinater og subtrahere startpunktets koordinater.
Eksempel 1:
I figuren over har vi punktene A = (4, 1), B = (2, 1), C = (1, 3), D = (3, 2), E = (−1, 1) og F = (1,0). Vi har derfor at
$\vec{AB} = [2 − 4, 1 −1] = [−2, 0]$
$\vec{CD} = [3 − 1, 2 −3] = [2, −1]$
$\vec{EF} = [1 − (−1), 0 −1] = [2, −1]$
Vi ser at koordinatene til vektorer angis mellom klammeparenteser.
Koordinatene til en vektor er uavhengige av hvor den befinner seg i koordinatsystemet. I figuren over har vi for eksempel at $\vec{CD} = \vec{EF} = [2, −1]$. Det betyr at $\vec{CD}$ og $\vec{EF}$ er samme vektor. Koordinatene [2, −1] betyr at når vi beveger oss langs vektoren, går vi 2 enheter i positiv retning langs x-aksen og 1 enhet i negativ retning langs y-aksen. I tilfellet $\vec{CD}$ går vi fra (1,3) til (3, 2), og i tilfellet $\vec{CD}$ går vi fra (−1, 1) til (1, 0).
Oppgave 1:
Vi har punktene G = (0, 4), L = (−2, 2), O = (2, 3) og R = (4, 4). Beregn koordinatene til vektorene $\vec{GL}$ og $\vec{OR}$.
Se løsningsforslag
Addere vektorer
Vi adderer to vektorer ved å addere koordinatene.
$\fbox{$\vec{a} + \vec{b} = [a_x + b_x, \; a_y + b_y]$}$
Eksempel 2:
Vi har vektorene $\vec{a} = [2, −3]$ og $\vec{b} = [2, 1]$, som vist under.

Vi får
$\vec{a}+ \vec{b} = [2 + 2, −3 + 1] = [4, −2]$
Dette tilsvarer vektoren som går fra starten av $\vec{a}$ til slutten av $\vec{b}$ hvis vi plasserer $\vec{b}$ etter $\vec{a}$:

Vektoraddisjon er kommutativ, det vil si at rekkefølgen vi adderer vektorene i, er uten betydning. For to vilkårlige vektorer, $\vec{a}$ og $\vec{b}$, vil altså
$\fbox{$\vec{a} + \vec{b} = \vec{b} + \vec{a}$}$
Eksempel 3:
Vi adderer vektorene $\vec{a} = [2, −3]$ og $\vec{b} = [2, 1]$ fra eksempel 2 i omvendt rekkefølge.
Vi får $\vec{b}+ \vec{a} = [2 + 2, 1 + (−3)] = [4, −2]$. Som er det samme som vi fikk i eksempel 2.
Dette tilsvarer vektoren som går fra starten av $\vec{b}$ til slutten av $\vec{a}$ hvis vi plasserer $\vec{a}$ etter $\vec{b}$

Vektoren er ikke plassert på samme sted i koordinatsystemet som i eksempel 2, men det har ingen betydning. Det er samme vektor, som går 4 enheter i positiv retning langs x-aksen og 2 enheter i negativ retning langs y-aksen.
Addisjon av vektorer kan vi illustrere med to menn som prøver å flytte en stein ved å dra i hvert sitt tau. Retningen og kraften av draget på steinen blir summen av vektorene som representerer draget fra hver mann, markert med grønt:

Vektoraddisjon er assosiativ, det vil si at hvis vi adderer mer enn to vektorer, spiller det ingen rolle hvilken rekkefølge vi adderer i. For tre vilkårlige vektorer, $\vec{a}$, $\vec{b}$ og $\vec{c}$, vil altså
$\fbox{$\vec{a} + (\vec{b} + \vec{c} ) = ( \vec{a} + \vec{b} ) + \vec{c}$}$
I praksis adderer vi alle koordinatene i samme operasjon.
Eksempel 4:
Vi har vektorene $\vec{a} = [1, 3]$, $\vec{b} = [−2, 4]$ og $\vec{c} = [2, 1]$, og skal beregne
$\vec{a} + \vec{b} + \vec{c}$
Vi får
$\vec{a} + \vec{b} + \vec{c} = [1 + (−2) + 2, 3 + 4 +1] = [1, 8]$
Oppgave 2:
Vi har vektorene $\vec{a} = [−3, 2]$, $\vec{b} = [4, 2]$ og $\vec{c} = [−1, −3]$.
Beregn
$\vec{a} + \vec{b} + \vec{c}$
Se løsningsforslag
Subtrahere vektorer
Vi subtraherer to vektorer ved å subtrahere koordinatene.
$\fbox{$\vec{a} − \vec{b} = [a_x − b_x, \; a_y − b_y]$}$
Eksempel 5:
Vi har vektorene $\vec{a} = [2, 4]$ og $\vec{b} = [3, 1]$, og skal beregne $\vec{a} − \vec{b}
Vi får
$\vec{a}− \vec{b} = [2 − 3, 4 − 1] = [−1, 3]$.
Dette vil være vektoren vi må legge til $\vec{b}$ for å få $\vec{a}$:
![]()

Vektorsubtraksjon er ikke kommutativ, men antikommutativ. Det vil si at hvis vi bytter om rekkefølgen på vektorene, bytter koordinatene i resultatet fortegn, slik at vektoren peker motsatt vei.
Eksempel 6:
Vi har vektorene $\vec{a} = [2, 4]$ og $\vec{b} = [3, 1]$, som i eksempel 5, og skal beregne $\vec{b} − \vec{a}$
Vi får
$\vec{b} − \vec{a} = [3 − 2, 1 − 4] = [1, −3]$, som er resultatet fra eksempel 5 med omvendt fortegn.
Dette vil være vektoren vi må legge til $\vec{a}$ for å få $\vec{b}$:

Additiv invers
For en vilkårlig vektor, $\vec{a}$, finnes det en invers vektor $\vec{−a}$, som er slik at $\vec{a} + (\vec{−a}) = \vec{0}$. Inverse vektorer har samme lengde, men peker i motsatt retning, slik som de grønne vektorene i henholdsvis eksempel 5 og 6. En vektors invers finner vi ved å skifte fortegn på koordinatene.
Vektoren $\vec{0}$ kalles en nullvektor og har ingen lengde.
Eksempel 7:
Vektorene $\vec{a} = [1, −3]$ og $\vec{−a} = [−3, 1]$ er additive inverser fordi
$\vec{a} +(\vec{−a}) = [1 + (−1), −3 +3] = [0, 0] = \vec{0}$
Lengden til en vektor
Lengden til en vektor er avstanden fra start- til sluttpunktet. På bildet under ser vi at en vektor i planet danner hypotenusen i en rettvinklet trekant, der katetene består av vektorens x– og y-koordinater.

Pytagoras′ setning gir oss derfor at lengden til en vektor i planet med koordinater $[x, y]$ blir $\sqrt{x^2 + y^2}$.
Eksempel 8:
Vi skal finne lengden til vektoren $\vec {a} = [3, 4]$
Vi får
$\sqrt{3^2 + 4^2} = \sqrt{25} = 5$.
Lengden til en vektor angis med absoluttverditegn. I eksempel 8 har vi for eksempel at $|\vec {a}| = 5$. Vi har altså at
$\fbox{$|\vec{a}| = \sqrt{{a_x}^2 + {a_y}^2}$}$
Det er ikke tilfeldig at vi bruker absoluttverditegn. Absoluttverdien til et vanlig, reelt tall forteller hvor langt tallet ligger fra 0, uavhengig av om det er positivt eller negativt. Plasserer vi en vektor med startpunktet i origo, forteller lengden hvor langt endepunktet er fra origo, uavhengig av hvilken vei vektoren peker. Lengden til en vektor er altså en utvidelse av absoluttverdibegrepet.
Oppgave 3:
Beregn $|\vec{b}|$ når $\vec{b} = [12, 5]$
Se løsningsforslag
At to vektorer har samme lengde, betyr ikke at de er like. For at to vektorer skal være like, må de i tillegg til å være like lange også peke i samme retning.
I bildet under er for eksempel $|\vec{a}| = |\vec{b}| = |\vec{c}|$, men bare $\vec{a} = \vec{c}$

Multiplisere vektor med skalar
Vi multipliserer en vektor med en skalar, altså et vanlig, reelt tall, ved å multiplisere koordinatene med tallet.
$\fbox{$k \vec{a} = [ka_x, \; ka_y]$}$
Lengden på vektoren skaleres da med tallet vi multipliserer med. Multipliserer vi med et negativt tall, skifter i tillegg vektoren retning.
Eksempel 9:
Vi har vektoren $\vec{a} = [1, 2]$. Da er
$2\vec{a} = [2 \cdot 1, 2 \cdot 2] = [2, 4]$
$\frac{1}{2}\vec{a} = [\frac{1}{2} \cdot 1, \frac{1}{2} \cdot 2] = [\frac{1}{2} , 1]$
$−\vec{a} = [−1 \cdot 1, −1 \cdot 2] = [−1, −2]$
$−2\vec{a} = [−2 \cdot 1, −2 \cdot 2] = [−2, −4]$
Dette er illustrert under.

Oppgave 4:
Gitt vektorene $\vec{a} = [3,1]$ og $\vec{b} = [−2,3]$
Beregn $2\vec{a} + 4 \vec{b}$
Se løsningsforslag
Multiplikasjon med skalar er distributiv under vektoraddisjon. Det vil si at vi for to vilkårlige vektorer, $\vec{a}$ og $\vec{b}$, og et vilkårlig, reelt tall, k, vil ha at
$\fbox{$k(\vec{a} + \vec{b}) = k\vec{a} + k\vec{b}$}$
Vi får altså samme resultat hvis vi multipliserer skalaren med summen av vektorene, som når vi multipliserer skalaren med hver av vektorene og deretter summerer.
Multiplikasjon med skalar er også distributiv under skalaraddisjon. Det vil si at vi for en vilkårlig vektor, $\vec{a}$, og to vilkårlige, reelle tall k og l, vil ha at
$\fbox{$(k + l)\vec{a} = k\vec{a} + l\vec{a}$}$
Vi får altså samme resultat hvis vi multipliserer summen av skalarene med vektoren, som når vi multipliserer hver av skalarene med vektoren og deretter summerer.
Mens vi for vanlig tallregning bare trenger én distributiv lov, trenger vi altså to for vektorregning. Én for distribusjon av vektorer og én for distribusjon av skalarer.
Skalarmultiplikasjon er assosiativ, så for en vilkårlig vektor, $\vec{a}$, og to vilkårlige, reelle tall, k og l, vil ha at
$\fbox{$ k(l\vec{a}) = (k l)\vec{a}$}$
Vi får altså samme resultat hvis vi multipliserer den ene skalaren med vektoren først og deretter med den andre skalaren, som når vi multipliserer skalarene først og deretter med vektoren.
Multiplisere vektorer
Vi har sett hvordan vi kan addere og subtrahere vektorer, og vi kan også multiplisere vektorer.
For vektorer er det definert to produkter.
Kryssprodukt
Den ene typen produkt er kryssproduktet. Kryssproduktet av to vektorer er en ny vektor som står vinkelrett på begge de opprinnelige vektorene og har lengde lik produktet av lengdene til de opprinnelige vektorene multiplisert med sinus til vinkelen mellom dem.
Kryssproduktet til to vektorer, $\vec{a}$ og $\vec{b}$, skriver vi som $\vec{a} \times \vec{b}$.
Siden kryssproduktet er en vektor, kalles kryssproduktet ofte også vektorproduktet.
For at en vektor skal kunne stå normalt på to andre, vilkårlige vektorer, må vi bevege oss ut av planet, slik det er illustrert under for $\vec{c} = \vec{a} \times \vec{b}$.

Kryssproduktet er antikommutativt, det vil si at
$\fbox{$\vec {a} \times \vec {b} = −(\vec {b} \times \vec {a})$}$
Bytter vi om faktorene, bytter kryssproduktet retning.
Kryssproduktet er ikke assosiativt, det vil si at generelt er
$\fbox{$\vec {a} \times (\vec {b} \times \vec {c}) \not = (\vec {a} \times \vec {b}) \times \vec {c}$}$
Kryssproduktet er et effektivt verktøy til å beregne areal og volum av romlegemer. Siden vi imidlertid i denne artikkelen holder oss til vektorer i planet, går vi ikke nærmere inn på kryssproduktet.
Prikkprodukt
Den andre typen produkt er prikkproduktet. Prikkproduktet til to vektorer i planet finner vi ved å multiplisere den ene vektorenes x-koordinat med den andres, og den ene vektorenes y-koordinat med den andres, og så summere produktene.
$\fbox{$\vec {a} \cdot \vec {b} = a_x \cdot b_x + a_y \cdot b_y$}$
Prikkproduktet er altså en skalar, og kalles derfor ofte også skalarproduktet. Vi holder oss imidlertid til navnet prikkprodukt for å unngå forveksling med skalarmultiplikasjon.
Eksempel 10:
Vi skal beregne prikkproduktet til vektorene $\vec{a} = [4,−1]$ og $\vec{b} = [5,3]$
Vi får
$\vec{a} \cdot \vec{b} = 4 \cdot 5 + (−1) \cdot 3 = 17$
Oppgave 5:
Beregn prikkproduktet til vektorene $\vec{a} = [4,2]$ og $\vec{b} = [−8,−4]$
Se løsningsforslag
Prikkproduktet er kommutativt. Det vil si at rekkefølgen vi multipliserer vektorene i, er uten betydning. For to vilkårlige vektorer, $\vec{a}$ og $\vec{b}$, har vi altså at
$\fbox{$\vec {a} \cdot \vec {b} = \vec {b} \cdot \vec {a}$}$
Siden prikkproduktet av to vektorer ikke er en vektor, men en skalar, gir det ingen mening å snakke om noen assosiativ lov for prikkproduktet. Men den distributive lov gjelder:
$\fbox{$(\vec {a} + \vec {b}) \cdot \vec {c} = \vec {a} \cdot \vec {c} + \vec {b} \cdot \vec {c} $}$
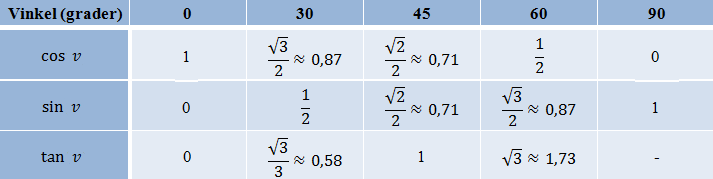
En annen måte å beregne prikkproduktet til to vektorer i planet på er å multiplisere lengdene til vektorene med cosinus til vinkelen mellom dem.
Kaller vi vinkelen mellom $\vec{a}$ og $\vec{b}$ for θ, har vi altså at
$\fbox{$\vec {a} \cdot \vec {b} = |\vec {a}| \cdot |\vec {b} | \cos \theta$}$
Eksempel 11:
Vi skal beregne prikkproduktet til vektorene $\vec{a} = [4,−1]$ og $\vec{b} = [5,3]$ fra eksempel 10 ved å benytte formelen over når vi vet at vinkelen mellom vektorene er 45°.
Vi vet at
$\cos 45^\circ = {\large \frac{\sqrt 2}{2}}$
og beregner
$|\vec{a}| = \sqrt{4^2 + (−1)^2} = \sqrt{17}$
og
$|\vec{b}| = \sqrt{5^2 + 3^2} = \sqrt{34}$
Så prikkproduktet blir
$\vec {a} \cdot \vec {b} =\sqrt{17} \cdot \sqrt{34} \cdot {\large \frac{\sqrt 2}{2}} = \sqrt{17} \cdot (\sqrt{17} \cdot \sqrt 2) \cdot {\large \frac{\sqrt 2}{2}} =$
$\sqrt{17} \cdot \sqrt{17} \cdot {\large \frac{\sqrt 2 \cdot \sqrt 2}{2}} = 17 \cdot {\large \frac{2}{2}} = 17$
Som er det samme vi fikk i eksempel 10.
Utregningen i eksempel 11 er jo mye mer innviklet enn den i eksempel 10, og det er jo sjelden at vi har et eksakt uttrykk for cosinus til en vinkel, så det kan ved første øyekast se ut til at vi bare har oppnådd å komplisere noe enkelt, men denne måten å beregne prikkproduktet på er svært nyttig i mange sammenhenger.
Oppgave 6:
Benytt metoden fra eksempel 11 til å beregne prikkproduktet av vektorene fra oppgave 5, $\vec{a} = [4,2]$ og $\vec{b} = [−8,−4]$, når du vet at vinkelen mellom vektorene er 180°.
Svaret skal bli det samme som i oppgave 5.
Se løsningsforslag
Ved å kombinere de to metodene, kan vi finne vinkelen mellom to vektorer.
Eksempel 12:
Vi skal finne vinkelen mellom vektorene $\vec{a} = [2,1]$ og $\vec{b} = [2,3]$
Vi har at (I)
$\vec {a} \cdot \vec {b} = a_x \cdot b_x + a_y \cdot b_y = 2\cdot 2 + 1 \cdot 3 = 7$
Samtidig har vi at (II)
$\vec {a} \cdot \vec {b} = |\vec {a}| \cdot |\vec {b} | \cos \theta = \sqrt{2^2 + 1^2} \cdot \sqrt{2^2 + 3^2} \cdot \cos \theta =$
$\sqrt{5} \cdot \sqrt{13} \cdot \cos \theta = \sqrt{65} \cdot \cos \theta$
Setter vi sammen (I) og (II), får vi
$7 =\sqrt{65} \cos \theta\Rightarrow \cos \theta = {\large \frac{7}{\sqrt{65}}}$
Så
$\theta = \cos^{−1}{\Big( {\large \frac{7}{\sqrt{65}}}}\Big) \approx 29{,}74^\circ$
Det er slik at for alle vinkler, v, er cos v = cos( −v).
Regner vi modulo 360°, får vi
cos( −v) = cos(−v + 360) = cos(360 −v)
Så det betyr at
θ ≈ 360 − 29,74° = 330,26°
også er en løsning i eksempel 12.
Dette er illustrert i figuren under:

Vi ser at vi får om lag 29,74° hvis vi måler fra $\vec {a}$ til $\vec {b}$, men om lag 330,26° hvis vi måler fra $\vec {b}$ til $\vec {a}$.
Når vi beregner vinkelen mellom vektorer, er det imidlertid naturlig å velge den minste vinkelen, som også er den vi får når vi beregner cos−1 θ på kalkulator eller datamaskin.
Oppgave 7:
Finn vinkelen (den minste) mellom vektorene $\vec{a} = [2,−1]$ og $\vec{b} = [1,3]$
Se løsningsforslag
Projisere vektorer
Vi nedfeller en normal fra enden av en vektor $\vec {a}$ på en vektor $\vec {b}$. Normalen vil da avgrense en ny vektor langs $\vec {b}$, som vi kaller projeksjonen av $\vec {a}$ på $\vec {b}$, og skriver som $\vec {a_b}$. Dette er illustrert under:

Denne vektoren vil være gitt som
$\fbox{$\vec{a_b} = \Big(\frac{\displaystyle \vec a \cdot \vec b}{\displaystyle \vec b \cdot \vec b}\Big)\vec b$}$
Det som står inni parentesen, er to prikkprodukter, som vi vet er skalarer. Projeksjonen skalerer altså $\vec {b}$, det vil si at den endrer lengden til vektoren $\vec {b}$. Skalering med et tall større enn 1 gjør vektoren lengre, skalering med et tall mellom 0 og 1 gjør vektoren kortere. Skalering med et negativt tall endrer også retning på vektoren.
Eksempel 13:
Vi skal beregne projeksjonen av $\vec a = [2, 4]$ på $\vec b = [6, 2]$, slik det er illustrert i figuren over.
Vi får
$\vec {a} \cdot \vec {b} = a_x \cdot b_x + a_y \cdot b_y = 2\cdot 6 + 4 \cdot 2 = 20$
og
$\vec {b} \cdot \vec {b} = b_x \cdot b_x + b_y \cdot b_y = 2\cdot 2 + 6 \cdot 6 = 40$
Så
$\vec{a_b} = \Big({\large \frac{20}{40}}\Big)[6,2] = [3,1]$
Beregner vi prikkproduktet i nevneren i formelen, får vi
$\vec b \cdot \vec b = b_x \cdot b_x + b_y \cdot b_y = (b_x)^2 + (b_y)^2$
Som er det samme som
$\Big(\sqrt{(b_x)^2 + (b_y)^2} \, \Big)^2 = \Big |\vec b|^2$
Vi dividerer altså med kvadratet av lengden til $\vec {b}$. Projeksjonen er derved uavhengig av lengden til $\vec {b}$, den avhenger bare av retningen.
Eksempel 14:
Vi krymper $\vec {b}$ fra eksempel 13 til $[{\large \frac{3}{2}}, {\large \frac{1}{2}}]$ og skal beregne projeksjonen av vektoren, $\vec a = [2, 4]$ fra eksempel 13, slik det er illustrert i figuren under:

Vi får
$\vec {a} \cdot \vec {b} = a_x \cdot b_x + a_y \cdot b_y = 2\cdot {\large \frac{3}{2}} + 4 \cdot {\large \frac{1}{2}} = 5$
og
$\vec {b} \cdot \vec {b} = b_x \cdot b_x + b_y \cdot b_y = {\large \frac{3}{2}}\cdot {\large \frac{3}{2}} +{\large \frac{1}{2}} \cdot {\large \frac{1}{2}} = {\large \frac{5}{2}}$
Så
$\vec{a_b} = \bigg({\large \frac{5}{\Large{\frac{5}{2}}}}\bigg)\Big[{\large \frac{3}{2}},{\large \frac{1}{2}}\Big] = 2\Big[{\large \frac{3}{2}},{\large \frac{1}{2}}\Big] = [3,1]$
Som er det samme som vi fikk i eksempel 13.
Oppgave 8:
Beregn projeksjonen av $\vec a = [−3, 2]$ på $\vec b = [4, 1]$
Se løsningsforslag
Vi avslutter med et gjensyn med vår venn som prøver å dra en stein.
La oss si at steinen ligger i ei grøft, og bare kan bevege seg rett mot høyre. Intuitivt vet vi at vi da bør dra i den retningen steinen kan bevege seg. Men la oss si at det ikke går an å gå i grøfta, men at mannen må gå litt på siden, slik:

Lar vi kraften mannen drar med, være symbolisert med en vektor, vil kraften som drar steinen i riktig retning være projeksjonen av denne ned på en vektor som går rett mot høyre, markert med grønt i figuren over. Jo lenger mannen går ut til siden, jo kortere blir projeksjonsvektoren, og jo mindre blir kraften som drar steinen i riktig retning.
































 Se film med løsningsforslag
Se film med løsningsforslag