Sjefen – Side 15 – nkhansen.com

1. mars 201821. januar 2025

Ekstremalpunkter

Finne stasjonære punkter

I artikkelen om polynomfunksjoner ser vi vi at en andregradsfunksjon, f(x) = ax² + bx + c, vil ha et topp- eller bunnpunkt når $x= −\frac{\displaystyle b}{\displaystyle 2a}$. Dette er fordi andregradsfunksjoner er symmetriske om sitt topp/bunnpunkt.

Andre funksjonstyper vil ikke ha så behagelige egenskaper. Da kan den deriverte komme oss til hjelp. Fordi den deriverte forteller hvor fort en funksjon endrer seg, må den deriverte i et topp- eller bunnpunkt være 0.

Eksempel 1:

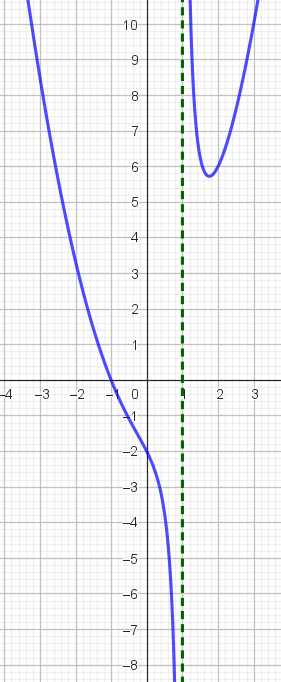
Under vises grafen til funksjonen f(x) = 2x³ + 3x² −12x + 4. Vi ser at den både har et toppunkt og et bunnpunkt.

Tredjegradsfunksjon med topp og bunnpunkt

Vi deriverer funksjonen, og får f′(x) = 6x² + 6x − 12.

Løser vi likningen

f′(x) = 6x² + 6x − 12 = 0, får vi

x₁ = 1 og x₂ = −2

De tilhørende funksjonsverdiene blir

f(1) = 2 · 1³ + 3 · 1² − 12 · 1 + 4 = −3

f(−2) = 2(−2)³ + 3(−2)² −12(−2) + 4 = 24

(Vi passer på å sette x-verdiene inn i den opprinnelige funksjonen, ikke i den deriverte.)

Av grafen ser vi at (−2, 24) er et toppunkt og (1, −3) er et bunnpunkt for f(x).

I stedet for toppunkt sier vi gjerne maksimumspunkt, og i stedet for bunnpunkt sier vi gjerne minimumspunkt. I et maksimumspunkt har altså funksjonen en maksimumsverdi, og i et minimumspunkt en minimumsverdi. Andre ord for det samme er maksimalpunkt og minimalpunkt og maksimalverdi og minimalverdi.

Et fellesnavn for maksimumspunkter og minimumspunkter er ekstremalpunkter. I slike punkter er den deriverte 0. Det finnes imidlertid enda en type punkt der den deriverte er 0:

Under vises grafen til f(x) = x³.

Tredjegradsfunksjon med terrassepunkt

Vi deriverer funksjonen, og får f′(x) = 3x². Den deriverte er 0 når x = 0, men vi ser at funksjonen verken har et maksimum eller minimum da, grafen flater bare ut litt, før den fortsetter i samme retning. Dette kaller vi et terrassepunkt.

Klassifisere stasjonære punkter

Et fellesnavn for ekstremalpunkter og terrassepunkter er stasjonære punkter. Funksjonsverdien endrer seg ikke der, den er stasjonær.

For å skille på de tre typene punkter kan vi studere hvordan fortegnet til den deriverte endrer seg. Vi har:

Maksimumspunkt. Den deriverte er 0 og skifter fortegn fra + til −.
Minimumspunkt. Den deriverte er 0 og skifter fortegn fra − til +.
Terrassepunkt. Den deriverte er 0, men skifter ikke fortegn.

Eksempel 2:

Funksjonen f(x) = x² + 4x −2 har derivert f′(x) = 2x + 4, som er 0 når x = −2. Det er lett å se at fortegnet er negativt når x < −2 og positivt når x > −2.

Siden fortegnet derved skifter fra − til + har vi et minimumspunkt i x = −2.

Den tilhørende funksjonsverdien blir

f(−2) = (−2)² + 4(−2) −2 = −6.

Så (−2, −6) er et minimumspunkt for f(x).

Siden den deriverte ikke er 0 andre steder enn i dette punktet, er det funksjonens eneste stasjonære punkt. Det stemmer med våre erfaringer med andregradsfunksjoner, som har ett enkelt topp- eller bunnpunkt.

For å avgjøre om vi har et maksimums-, minimums- eller terrassepunkt, studerer vi altså hva som skjer med den derivertes fortegn i punktet. Vi kan ikke konkludere med noe bare ved å se på funksjonsverdien alene. Det er nemlig ikke alltid slik at punktet med høyest funksjonsverdi er et maksimum, og punktet med lavest funksjonsverdi er et minimum. Dette er illustrert under.

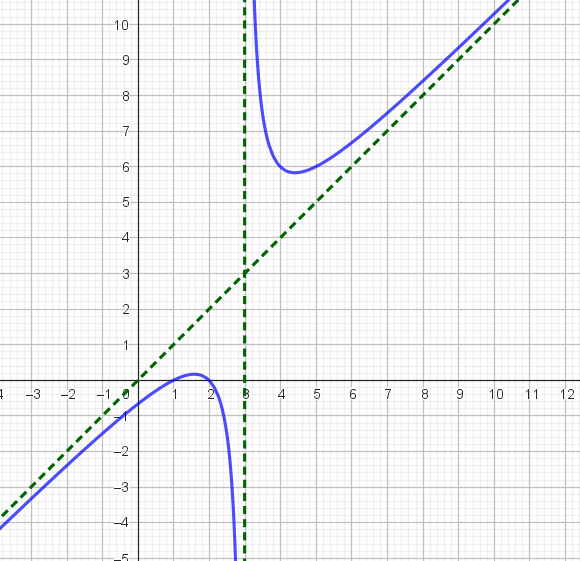
Eksempel 3:

Under vises grafen til den rasjonale funksjonen $f(x) = {\large \frac{x^2−x+1}{1−x}}$.

Minimumspunktet har funksjonsverdi 1, mens maksimumspunktet har funksjonsverdi −3.

Illustrasjon av et makspunkt ikke trenger ha størst funksjonsverdi

Å se hvordan den deriverte skifter fortegn er imidlertid ikke alltid like lett som eksempel 2. I mer sammensatte tilfeller må vi faktorisere den deriverte, og så lage et fortegnsskjema. Fortegnsskjema presenteres i artikkelen om likninger og ulikheter av høyere grad, der det blir brukt som en hjelp til å løse ulikheter.

Eksempel 4:

I eksempel 1 fant vi at (−2, 24) er et maksimumspunkt og (1, −3) et minimumspunkt for funksjonen f(x) = 2x³ + 3x² −12x + 4 ved å studere grafen. Nå skal vi se hvordan vi kan bruke fortegnsskjema til å komme fram til det samme. Den deriverte er altså

f′(x) = 6x² + 6x − 12, med nullpunkter i x₁ = 1 og x₂ = −2.

Som det beskrives i artikkelen om å faktorisere polynomer, betyr dette at 6x² + 6x − 12 kan faktoriseres som 6(x − 1)(x + 2).

Vi tegner faktorene (x − 1) og (x + 2) inn i et fortegnsskjema, der vi markerer negative verdier med en prikket linje og positive verdier med en heltrukken linje. (Faktoren 6 er alltid positiv, så vi bryr oss ikke om å ta den med.) Har faktorene har samme fortegn, er produktet positivt, har de forskjellig fortegn, er produktet negativt. Dette markerer vi med en linje for produktet, altså (x − 1)(x + 2) :

Bruk av fortegnsskjema til å bestemme fortegnet på derivert

Vi ser at fortegnet til (x − 1)(x + 2) skifter fra + til − i x = −2 og fra − til + i x = 1.

x = −2 og x = 1 er derfor henholdsvis maksimum og minimum for f(x).

Oppgave 1:

Bruk derivasjon og fortegnsskjema til å finne og klassifisere de stasjonære punktene til $f(x) = {\large \frac{1}{3}}x^3 − {\large \frac{1}{2}}x^2 −6x + 2$.

Med å klassifisere punktene mener vi å avgjøre om de er maksimums-, minimums-, eller terrassepunkter.

Se løsningsforslag

Ikke alle funksjoner har stasjonære punkter.

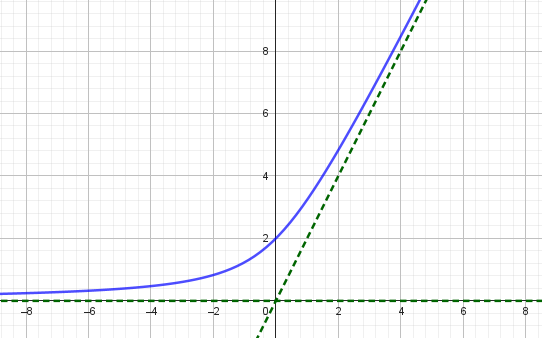
Eksempel 5:

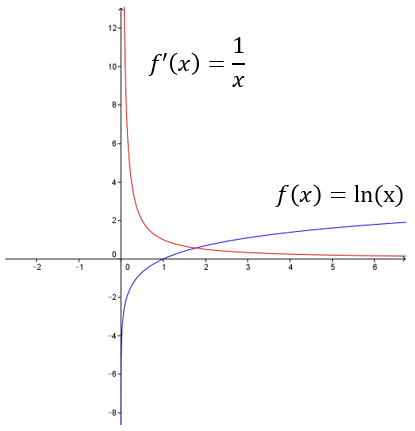
Gitt funksjonen $f(x) = \ln x$, med derivert $f′(x) = {\large \frac{1}{x}}$. Den deriverte skifter riktig nok fortegn når x = 0, men definisjonsområdet til ln x er x > 0. Den deriverte er derved alltid positiv i definisjonsområdet, og funksjonen har ingen stasjonære punkter.

Grafene til $f(x) =\ln x$ og $f′(x) = {\large \frac{1}{x}}$ er vist under.

Grafen til ln x og den deriverte

Oppgave 2:

Bruk derivasjon til å avgjøre om funksjonen $f(x) = {\large \frac{1}{x}}$ har noen ekstremalpunkter.

Se løsningsforslag

I GeoGebra kan vi finne en funksjons ekstremalpunkter ved hjelp av funksjonen Ekstremalpunkt.

En funksjon kan naturligvis ha mer enn ett maksimumspunkt og ett minimumspunkt.

Eksempel 6:

Grafen under viser en funksjon med tre ekstremalpunkter. (Utenfor bildet fortsetter grafen mot minus uendelig på begge sider.)

Graf med flere maksimumspunkter

Vi ser at både A og C er maksimumspunkter, mens B er et minimumspunkt.

Lokale og globale ekstremalpunkter

Vi skiller mellom lokale og globale punkter. Et globalt maksimumspunkt er et punkt der funksjonsverdien når sitt absolutte maksimum i hele definisjonsområdet. I eksempel 6 ser vi at C er et slikt punkt. Et lokalt maksimumspunkt er et punkt der funksjonsverdien når sitt maksimum innenfor et intervall. I eksempel 6 ser vi at både A og C er slike punkter.

Et globalt maksimumspunkt er også et lokalt maksimumspunkt, men for enkelhets skyld refererer vi bare til det som et globalt maksimumspunkt.

En funksjon kan godt ha flere globale maksimumspunkter, det vil si at funksjonsverdien når sitt absolutte maksimum for flere x-verdier. f(x) = sin x er et eksempel på en funksjon med uendelig mange globale maksimumspunkter. Funksjonsverdien når sitt absolutte maksimum på 1 for x = 90°, x = 450°, x = 810°, …

Med minimumspunkter forholder det seg på nøyaktig samme måte. Et globalt minimumspunkt er et punkt der funksjonsverdien når sitt absolutte minimum i hele definisjonsområdet. I eksempel 6 fortsetter grafen mot minus uendelig utenfor bildet, og det finnes derfor ikke noe globalt minimumspunkt. Derimot er B et lokalt minimumspunkt.

Et globalt minimumspunkt er også et lokalt minimumspunkt, men for enkelhets skyld refererer vi bare til det som et globalt minimumspunkt.

En funksjon kan godt ha flere globale minimumspunkter, det vil si at funksjonsverdien når sitt absolutte minimum for flere x-verdier. f(x) = sin x er et eksempel på en funksjon med uendelig mange globale minimumspunkter. Funksjonsverdien når sitt absolutte minimum på −1 for x = 270°, x = 630°, x = 990°, …

Formelt kan vi oppsummere dette slik:

En funksjon, f(x), har et globalt maksimumspunkt i f(c) hvis f(c) ≥ f(x) for alle x i definisjonsmengden, D_f.
En funksjon, f(x), har et globalt minimumspunkt i f(c) hvis f(c) ≤ f(x) for alle x i definisjonsmengden, D_f.
En funksjon, f(x), har et lokalt maksimumspunkt i f(c) hvis f(c) ≥ f(x) for alle x i et intervall rundt c.
En funksjon, f(x), har et lokalt minimumspunkt i f(c) hvis f(c) ≤ f(x) for alle x i et intervall rundt c.

Kritiske punkter

Hvis vi avgrenser definisjonsmengden til en funksjon, vil vi også endepunktene bli ekstremalpunkter. Disse kan være globale eller bare lokale.

Eksempel 7:

Grafen under har 6 ekstremalpunkter.

Ekstremalpunkter i graf med endepunkter

Globalt maksimumspunkt: C. Lokale maksimumspunkter: A og F.

Globalt minimumspunkt: E. Lokale minimumspunkter: B og D.

Punktene der en funksjon kan ha ekstremalpunkter, kalles kritiske punkter. Dersom en funksjon er definert på et intervall [a, b], vil kritiske punkter være:

x = a og x = b
Punkter der den deriverte er 0
Punkter der den deriverte ikke er definert.

For å finne en funksjons ekstremalpunkter, går vi fram på følgende måte:

Vi finner funksjonens kritiske punkter.
Vi bruker fortegnsskjema til å klassifisere punktene.
Vi undersøk funksjonsverdien i de kritiske punktene for å avgjøre hvilke av dem som er globale.

I endepunktene til definisjonsområdet har vi jo ikke noe fortegnsskifte til den deriverte, men siden en positiv derivert betyr at funksjonsverdien stiger og en negativ derivert betyr at funksjonsverdien avtar, er det allikevel lett å klassifisere disse punktene.

Eksempel 8:

Vi skal finne alle ekstremalpunkter til funksjonen $f(x) = {\large \frac{1}{3}}x^3 + x^2 −3x$, $D_f = [−6, 2]$.

Vi starter med å derivere funksjonen, og får

f′(x) = x² + 2x − 3.

Vi løser likningen f′(x) = x² + 2x − 3 = 0 og får

x₁ = 1, x₂ = −3.

Det vil si at den deriverte kan faktoriseres som f′(x) = 1(x − 1)(x + 3). Vi lager fortegnsskjema:

Bruk av fortegnsskjema til å bestemme fortegnet på derivert

Vi ser at x = −6 er et minimum fordi den deriverte er positiv ut fra dette punktet, slik at funksjonen stiger. Funksjonsverdien i punktet blir

$f(−6) = {\large \frac{1}{3}}(−6)^3 + (−6)^2 −3(−6) = −18$

Vi ser at x = −3 er et maksimum fordi den deriverte skifter fra positiv til negativ i dette punktet. Funksjonsverdien i punktet blir

$f(−3) = {\large \frac{1}{3}}(−3)^3 + (−3)^2 −3(−3) = 9$

Vi ser at x = 1 er et minimum fordi den deriverte skifter fra negativ til positiv i dette punktet. Funksjonsverdien i punktet blir

$f(1) = {\large \frac{1}{3}}1^3 + 1^2 −3\cdot 1 = −{\large \frac{5}{3}}$

Vi ser at x = 2 er et maksimum fordi den deriverte er positiv inn mot dette punktet, slik at funksjonen stiger. Funksjonsverdien i punktet blir

$f(2) = {\large \frac{1}{3}}2^3 + 2^2 −3\cdot 2 = {\large \frac{2}{3}}$

Vi ser at 9 er høyeste funksjonsverdi og −18 laveste. Vi får derfor at (−6, −18) er globalt minimumspunkt, (−3, 9) er globalt maksimumspunkt, $(1, −{\large \frac{5}{3}})$ er lokalt minimumspunkt, $(2, {\large \frac{2}{3}})$ er lokalt maksimumspunkt.

Grafen til funksjonen med ekstremalpunktene markert er vist under.

Graf som illustrerer resuktatene fra funksjonsdrøfting

Oppgave 3:

Finn og klassifiser alle ekstremalpunktene til $f(x) = {\large \frac{1}{3}}x^3 − {\large \frac{1}{2}}x^2 −6x + 2$, $D_f = [−5, 5]$.
Hint: Du klassifiserte de stasjonære punktene til denne funksjonen i oppgave 1. Det kan du bygge videre på.

Se løsningsforslag

En funksjon som er definert på et lukket intervall, [a, b], og er kontinuerlig på intervallet, vil alltid ha minst ett globalt maksimumspunkt og minst ett globalt minimumspunkt. Dette er intuitivt rimelig. På en kontinuerlig graf mellom to punkter må det jo være noe som er øverst og nederst.

For en ikke-kontinuerlig funksjon er vi imidlertid ikke garantert å ha globale ekstremalpunkter, som vist i eksempel 9.

Eksempel 9:

Grafen til $f(x) = {\large \frac{1}{x}}$, $D_f = [−5, 5]$ er vist under.

Grafen til 1/x på avgrenset område

Vi ser at funksjonen har et lokalt maksimum i x = −5 og et lokalt minimum i x = 5, men den har ingen globale ekstremalpunkter. Grafen går mot både pluss og minus uendelig ved x = 0.

Kilder

- Gulliksen, T. & Hole, A. (2010). Matematikk i praksis. Universitetsforlaget
- Thomas, G.B., Finney R.L. (1988). Calculus and Analytic Geometry. Addison-Wesley.
- matematikk.org

2. mars 201821. januar 2025

Høyere ordens deriverte

Gjentatt derivasjon

Vi nøyer oss i mange artikler med å derivere funksjoner én gang. Nå skal vi se hva vi kan få ut av å derivere flere ganger.

Vi har brukt en apostrof til å angi at vi deriverer, og skrevet den deriverte til en funksjon, f, som f′. For å angi at vi deriverer to ganger, bruker vi to apostrofer, og skriver den andrederiverte som f′′. For å angi at vi deriverer tre ganger, bruker vi tre apostrofer, og skriver den tredjederiverte som f′′′. Slik kan vi fortsette å fylle på med apostrofer, men det blir fort uleselig. I stedet bruker vi derfor et tall, n, i parentes for å angi den n−te−deriverte. f⁽⁴⁾ for den fjerdederiverte, f⁽⁵⁾ for den femtederiverte, og så videre. Det finnes allikevel ingen absolutt regel som sier at vi skal skifte fra apostrof til tall når vi deriverer mer enn tre ganger, det er helt greit å skrive f⁽²⁾ for den andrederiverte og f′′′′ for den fjerdederiverte.

Eksempel 1:

Vi har funksjonen f(x) = x⁴ − 3x² + 5x. De deriverte blir

f′(x) = 4x³ − 6x + 5

f′′(x) = 12x² − 6

f′′′(x) = 24x

f ⁽⁴⁾(x) = 24

f ⁽⁵⁾(x) = 0

Den andrederiverte

I denne artikkelen skal vi holde oss til å se på den andrederiverte, som gir nyttige opplysninger om en funksjon. Den andrederiverte kalles også for den dobbeltderiverte.

Vi sier i andre artikler at den deriverte forteller om hvordan en funksjon endrer seg. Er den deriverte positiv, er funksjonen voksende, er den negativ, er den avtakende. Ved å se på den andrederiverte, kan vi avgjøre funksjonens krumningsegenskaper, altså om den er konveks eller konkav. Er den konveks, vender grafen sin hule side opp, er den konkav, vender grafen sin hule side ned. Funksjonen er konveks hvis f′′ > 0 og konkav hvis f′′ < 0. Et punkt der funksjonen skifter fra konveks til konkav eller omvendt kalles et vendepunkt.

Eksempel 2:

Vi studerer funksjonen $f(x) = {\large \frac{1}{3}}x^3 − 2x^2 + 3x +1$.

Vi deriverer, og får at f′(x) = x² − 4x + 3.

Vi tar ikke med utregningene her, men fortegnet til den deriverte skifter fra + til − når x = 1, og dette er derfor et maksimum. Fortegnet skifter fra − til + når x = 3, og dette er derfor et minimum.

Vi deriverer en gang til, og får at f′′(x) = 2x −4.

Fortegnet til den andrederiverte skifter fra − til + når x = 2. Dette er derfor et vendepunkt, der funksjonen går over fra å være konkav (hule side ned) til konveks (hule side opp).

Dette er illustrert i grafen under. Til venstre for den røde, stiplede linja er funksjonen konkav, til høyre for linja, konveks.

Graf med illustrasjon av ekstremalpunkter og vendepunkt

At funksjonen er konkav, betyr at grafen er i ferd med å vri seg nedover, at den er konveks betyr at den er i ferd med å vri seg oppover. En regel for å huske hva som er hva, kan derfor være at «konveks gir vekst».

I GeoGebra kan vi finne en funksjons vendepunkter med kommandoen vendepunkt.

Den deriverte beskriver altså hvordan en funksjon endrer seg. En positiv derivert betyr at funksjonen er voksende, en negativ at den er avtagende. Den andrederiverte forteller naturligvis nøyaktig det samme om den deriverte. En positiv andrederivert betyr at den deriverte er voksende, en negativ at den er avtagende. Bildet under viser funksjonen fra eksempel 2, der vi i tillegg har tatt med grafen til f′, vist med oransje og grafen til f′′, vist med grønt.

Grafer som illustrerer sammenhengen mellom funksjon,derivert og andrederivert

Vi ser at den opprinnelige funksjonen har ekstremalpunkter der hvor den deriverte er 0, altså i x = 1 og x = 3. Den deriverte på sin side har et ekstremalpunkt der den andrederiverte er 0, altså i x = 2. Siden fortegnet til den andrederiverte der skifter fra − til +, er dette et minimumspunkt. Dette minimumspunktet korresponderer med den opprinnelige grafens vendepunkt.

Hvis vi går fra venstre inn mot dette punktet, ser vi at den deriverte blir mer og mer negativ. Det betyr at den opprinnelige funksjonen avtar raskere og raskere. Når punktet er passert, er den deriverte fortsatt negativ, så den opprinnelige funksjonen fortsetter å avta, men nå blir den deriverte mindre og mindre negativ, så raten den avtar i blir langsommere og langsommere. Når så den deriverte passerer 0, blir den mer og mer positiv, så den opprinnelige funksjonen vil stige raskere og raskere.

Eksempel 3:

En bedrift har funnet ut at fortjenesten de får ved å produsere og selge en vare er gitt, i millioner kroner, ved funksjonen $f(t) = {\large \frac{1}{3}}t^3 − 2t^2 + 3t −2$, der t er antall år siden varen ble lansert på markedet.

De gjør en vurdering av situasjonen etter 2,5 år. Fortjenesten er da f(2,5) ≈ −1,79. Bedriften taper penger på varen.

Den deriverte til fortjenestefunksjonen er f′(t) = t² − 4t + 3. Etter 2,5 år har vi at f′(2,5) = −0,75. Den deriverte er altså negativ. Det betyr at fortjenestefunksjonen er avtagende. Bedriftens utsikter er altså at de ikke bare kommer til å fortsette å tape penger, men at de vil tape mer og mer.

Den andrederiverte til fortjenestefunksjonen er f′′(t) = 2t − 4. Etter 2,5 år har vi at f′′(2,5) = 1. Den andrederiverte er altså positiv, og vi ser at den vil fortsette å være positiv for økende t. Det betyr at selv om den deriverte er negativ, er den voksende, og vil på et tidspunkt passere 0. Det betyr at selve fortjenestefunksjonen vil gå over fra å være avtagende til å være voksende, og på et tidspunkt vil den også passere 0, slik at bedriften går over fra å tape til å tjene penger.

En funksjon kan selvfølgelig ha mer enn ett vendepunkt. f(x) = sin x har for eksempel uendelig mange vendepunkter, og veksler fram og tilbake mellom konveks og konkav hver gang f′′(x) = −sin x passerer 0, det vil si x = 0°, x = 180°, x = 360°, …

På den annen side finnes det funksjoner som ikke har vendepunkter. f(x) = e^x for eksempel, har andrederivert f′′(x) = e^x , en funksjon som alltid er positiv. f(x) = e^x er derfor konveks (krummer oppover) i hele definisjonsområdet. En vilkårlig andregradsfunksjon, f(x) = ax² + bx + c, har andrederivert f′′(x) = 2a og er konveks i hele definisjonsområdet hvis a > 0, konkav hvis a < 0.

Oppgave 1:

Finn og klassifiser vendepunktene til $f(x) = {\large \frac{1}{12}}x^4 − {\large \frac{1}{6}}x^3 − x^2 + x + 1$.

Med å klassifisere vendepunktene mener vi å angi om funksjonen skifter fra konkav til konveks eller omvendt i punktet.

Se løsningsforslag

Oppgave 2:

Finn og klassifiser vendepunktene til f(x) = (x² − 3x + 2)e^x. Denne funksjonen har vendepunkter, selv om GeoGebra svarer «Udefinert» hvis vi prøver å bruke vendepunkt-kommandoen.

Se løsningsforslag

Derivasjon med GeoGebra

GeoGebra har kommandoer for å derivere en funksjon en eller flere ganger:

- Derivert: derivert(f) eller f′(x).
- Andrederivert: derivert(f, 2) eller f′′(x).
- Tredjederivert: derivert(f, 3) eller f′′′(x).
- n-te-derivert: derivert(f, n) eller f^{n apostrofer}(x) der n er et positivt helt tall.

Her er f navnet på funksjonen vi skal derivere, og x navnet på den uavhengige variabelen.

GeoGebra viser funksjonsforskriften til den deriverte i algebrafeltet og tegner grafen i grafikkfeltet.

GeoGebra følger dessverre ikke konvensjonen med å sette inn et tall for å angi deriverte av høyere orden enn 3, for eksempel f⁽⁴⁾(x) for den fjerdederiverte til f(x). I stedet fylles bare på med apostrofer. Dette blir litt uoversiktlig.

Andrederivert-testen

I eksempel 4 i artikkelen om ekstremalpunkter bruker vi fortegnsskjema til å klassifisere ekstremalpunktene til f(x) = 2x³ + 3x² − 12x + 4. Vi kom fram til at funksjonen har et maksimumspunkt i x = −2 fordi den deriverte skifter fortegn fra + til − i dette punktet, og at funksjonen har et minimumspunkt i x = 1 fordi den deriverte skifter fortegn fra − til + i dette punktet.

Grafen til funksjonen er vist under:

Graf som illustrerer sammenhengen mellom krumningsegenskaper og klassifisering av ekstremalpunkter

Vi ser at i maksimumspunktet er funksjonen konkav, og i minimumspunktet er funksjonen konveks. Dette er ikke tilfeldig. Det vil alltid være slik at et ekstremalpunkt der funksjonen er konkav, er et maksimumspunkt, og et ekstremalpunkt der funksjonen er konveks, er et minimumspunkt.

For å klassifisere et stasjonært punkt, har vi derved et alternativ til å undersøke fortegnet til den deriverte. Det kalles andrederivert-testen.

$\fbox{$\begin{align} &\text{Hvis }f′(c) = 0 \text{ og } f′\,′(c) < 0 \text{, har } f \text{ et maksimumspunkt i } x = c \\
&\text{Hvis }f′(c) = 0 \text{ og } f′\,′(c) > 0 \text{, har } f \text{ et minimumspunkt i } x = c \end{align}$}$

Eksempel 4:

Funksjonen f(x) = x² + 4x −2, som vi også ser på i eksempel 2 i artikkelen om ekstremalpunkter, har derivert f′(x) = 2x + 4 og andrederivert f′′(x)= 2.

f′(x) er 0 når x = −2, så dette er et stasjonært punkt.

f′′(−2) = 2 > 0, så punktet er et minimumspunkt.

Eksempel 5:

Funksjonen $f(x) = {\large \frac{1}{3}}x^3 + x^2 −3x$, som vi også ser på i eksempel 8 i artikkelen om ekstremalpunkter, har derivert f′(x) = x² + 2x − 3 og andrederivert f′′(x) = 2x + 2.

Den deriverte kan faktoriseres som f′(x) = (x − 1)(x + 3).

f′(x) er 0 når x = −3, så dette er et stasjonært punkt.

f′′(−3) = 2(−3) + 2 = −4 < 0, så punktet er et maksimumspunkt.

f′(x) er 0 når x = 1, så dette er et stasjonært punkt.

f′′(1) = 2 · 1 + 2 = 4 > 0, så punktet er et minimumspunkt.

Oppgave 3:

Finn de stasjonære punktene til f(x) = 2x³ − 9x² + 12x − 2, og bruk andrederivert-testen til å klassifisere dem.

Se løsningsforslag

Andrederivert-testen klassifiserer altså et stasjonært punkt som et maksimumspunkt hvis den andrederiverte er mindre enn null, og som et minimumspunkt hvis den andrederiverte er større enn null.

Men det er ikke slik at testen klassifiserer et stasjonært punkt som et terrassepunkt hvis den andrederiverte er lik null. Andrederivert-testen gir ikke svar hvis f′′ = 0.

Eksempel 6

De deriverte til f(x) = x⁴, g(x) = −x⁴ og h(x) = x³ er alle null når x = 0, så funksjonene har stasjonære punkter da. Disse punktene er henholdsvis minimumspunkt, maksimumspunkt og terrassepunkt. Men den andrederiverte er null i alle tre tilfeller, så andrederivert-testen gir ikke svar. For å kunne klassifisere punktene, må vi studere fortegnet til den deriverte.

Om vi skal velge andrederivert-testen eller å studere fortegnet til den deriverte når vi skal klassifisere et stasjonært punkt, vil avhenge av situasjonen. Det er altså ikke alltid at andrederivert-testen fungerer, og av og til kan det være komplisert å finne den andrederiverte. Da velger vi å studere fortegnet. Er det derimot lett å finne den andrederiverte og vanskelig å finne ut av fortegnsskiftet til den deriverte, velger vi andrederivert-testen. Av og til er vi uansett nødt til å finne den andrederiverte fordi vi trenger den til å finne vendepunkter og å avgjøre hvor funksjonen er konveks og konkav. Da kan vi jo like godt også bruke den til andrederivert-testen.

Kilder

- Gulliksen, T. & Hole, A. (2010). Matematikk i praksis. Universitetsforlaget
- Thomas, G.B., Finney R.L. (1988). Calculus and Analytic Geometry. Addison-Wesley.
- matematikk.org

28. februar 201821. januar 2025

Kombinere derivasjonsregler

I mange artikler lærer vi om derivasjon av forskjellige typer funksjoner, derivasjon av uttrykk som består av summer, differanser, produkter og kvotienter av disse funksjonene og funksjoner inni funksjoner. Ofte vil vi imidlertid støte på uttrykk som krever bruk av flere regler etter hverandre, eller bruk av samme regel flere ganger. Vi trenger ikke lære noe nytt for å gjøre dette, det holder å bruke de reglene vi allerede kan, på en systematisk måte. Det som kan være krevende er å finne ut rekkefølgen de skal brukes i. Et greit prinsipp er da, på samme måte som ved kjerneregelen, å se etter uttrykk som vi har regler for å derivere.

Eksempel 1:

Vi skal derivere funksjonen f(x) = x · ln 2x.

Dette er et produkt, som vi kjenner regelen for å derivere:

f′(x) = x′ · ln 2x + x · (ln 2x)′.

Men vi har ingen regel for å derivere ln 2x. Her må vi bruke kjerneregelen:

Vi har at den ytre funksjonen er f(g) = ln g, og den indre funksjonen er g(x) = 2x.

Kjerneregelen gir

$(\ln 2x)′ = (\ln g)′ \cdot (2x)′ = \frac{\displaystyle 1}{\displaystyle g} \cdot 2 = \frac{\displaystyle 2}{\displaystyle 2x} = \frac{\displaystyle 1}{\displaystyle x}$

Så vi har at

$ f′(x) = x′ \cdot \ln 2x + x \cdot (\ln 2x)′ = 1 \cdot \ln 2x + x \cdot \frac{\displaystyle 1}{\displaystyle x} = \ln 2x + 1$

Eksempel 2:

Vi skal derivere funksjonen $f(x) = e^{\large \sin x^2}$

Her må vi bruke kjerneregelen to ganger etter hverandre. For å holde de to kjernene fra hverandre, kaller vi dem g og h, der g = sin h, og h = x².

$f′(x) = (e^g)′ \cdot (\sin x^2)′ = (e^g)′ \cdot (\sin h)′ \cdot (x^2)′ =$

$e^g \cdot \cos h \cdot 2x= e^{\large \sin x^2} \cdot \cos x^2 \cdot 2x$

Oppgave 1:

Deriver funksjonen f(x) = sin 2x cos 2x.

Se løsningsforslag

Oppgave 2:

Deriver funksjonen $f(x) = \frac{\displaystyle e^x \ln x}{\displaystyle x^2}$

Se løsningsforslag

Oppgave 3:

Dette er en krevende oppgave for dem som ønsker en ekstra utfordring.

Uttrykket $\frac{\displaystyle u}{\displaystyle v}$, der u og v er to vilkårlige funksjoner, kan skrives som u · v⁻¹. Benytt dette, produktregelen og kjerneregelen til å utlede kvotientregelen, altså at

$\Big( \frac{\displaystyle u}{\displaystyle v} \Big)′ = \frac{\displaystyle u′v − uv′}{\displaystyle v^2}$

Se løsningsforslag

Kilder

- Gulliksen, T. & Hole, A. (2010). Matematikk i praksis. Universitetsforlaget
- Thomas, G.B., Finney R.L. (1988). Calculus and Analytic Geometry. Addison-Wesley.
- matematikk.org

27. februar 20181. februar 2025

Derivere funksjonskombinasjoner

I artikkelen om å derivere potensfunksjoner og artikkelen om å derivere ulike typer funksjoner ser vi hvordan vi deriverer potensfunksjoner, trigonometriske funksjoner, eksponentialfunksjoner og logaritmefunksjoner. Nå skal vi se på regler for hvordan vi deriverer kombinasjoner av funksjoner.

Litt om notasjon

I alle reglene bruker vi en funksjon som vi kaller f(x), og i de fleste også en funksjon vi kaller g(x). Denne notasjonen er den mest presise, men de forskjellige uttrykkene kan bli litt komplekse og vanskelige å tolke. Vi angir derfor også reglene på en kortform, der vi kaller funksjonene u og v.

Rekkefølgen på ledd er likegyldig, (u)′v + u(v)′ er det samme som u(v)′ + (u)′v. Rekkefølgen på faktorer er også likegyldig, u(v)′ er det samme som (v)′u. I denne artikkelen bruker vi praksis fra matematikk.net. Men det finnes ikke noen entydig standard. Innholdet i reglene er imidlertid alle tilfeller de samme.

Konstantregelen

Den første regelen er den enkleste. Hvis vi skal derivere en funksjon multiplisert med en konstant, kan vi sette konstanten utenfor derivasjonen:

$\fbox{$\big(kf(x)\big)′ = kf′(x)$}$

På kortform:

$\fbox{$\big(ku\big)′ = ku′$}$

Eksempel 1:

(5x²)′ = 5(x²)′ = 5(2x) = 10x.

Sum- og differanseregelen

Å derivere en sum eller differanse av funksjoner er også enkelt, vi deriverer funksjonene hver for seg:

$\fbox{$\big(f(x) \pm g(x) \big)′ = f′(x) \pm g′(x)$}$

På kortform:

$\fbox{$\big(u \pm v \big)′ = u′ \pm v′$}$

Eksempel 2:

(x⁴ + x³ − x²)′ = (x⁴)′ + (x³)′ − (x²)′ = 4x³ + 3x² − 2x.

Ved hjelp av disse to reglene kan vi nå derivere alle polynomfunksjoner.

Eksempel 3:

Vi skal derivere f(x) = −3x² + 2x − 8.

Vi får

f′(x) = (−3x²)′ + (2x)′ − (8)′ = −3(x²)′ + 2(x)′ − (8)′ = −3 · 2x + 2 · 1 − 0 = −6x +2.

Her har vi ført utregningen ytterst omstendelig for å illustrere hvilke regler som brukes. Men det meste av utregningen kan utføres i hodet. Vi tar for oss ledd for ledd, flytter eksponenten ned og multipliserer med en eventuell koeffisient, før vi reduserer eksponenten med 1.

Vi kunne skrevet det så kort som

f′(x) = −3 · 2x + 2 · 1 − 0 = −6x +2.

Alle polynomfunksjoner er deriverbare for alle x.

Oppgave 1:

Deriver funksjonene under:

- f(x) = 2x³ − 5x² + 4x − 1
- f(t) = t⁵ − 3t² + 7t

Se løsningsforslag

Produktregelen

Å derivere et produkt av to funksjoner er litt mer komplisert enn å derivere en sum eller differanse av to funksjoner:

$\fbox{$\big(f(x) \cdot g(x) \big)′ = f′(x) \cdot g(x) + f(x) \cdot g′(x)$}$

På kortform:

$\fbox{$\big(uv \big)′ = u′v +uv′$}$

Vi deriverer altså ved å multiplisere den ene funksjonen med den deriverte av den andre, og vice versa, og så addere de to produktene.

Eksempel 4:

(x⁴ · x³)′ = (x⁴)′ · x³ + x⁴ · (x³)′ = 4x³ · x³ + x⁴ · 3x² = 7x⁶.

Denne utregningen kan vi lett kontrollere ved å beregne uttrykket inni parentesen før vi deriverer:

(x⁴ · x³)′ = (x⁷)′ = 7x⁶.

I eksempel 4 var det bakvendt å bruke produktregelen fordi vi kunne gjøre derivasjonen mye enklere ved å multiplisere ut uttrykket i parentesen først. Men en slik forenkling vil ofte ikke være mulig.

Eksempel 5:

Vi skal derivere funksjonen f(x) = x² sin x.

Her har vi et produkt av en potensfunksjon og en trigonometrisk funksjon som ikke kan forenkles, og vi må bruke produktregelen. Vi får:

f′(x) = (x²)′ sin x + x² (sin x )′ = 2x sin x + x² cos x.

Oppgave 2:

Deriver funksjonen f(x) = (3x² + 7x)(4x⁵ + 2x³) både ved å bruke produktregelen direkte, og ved å multiplisere sammen parentesene før du deriverer.

Se løsningsforslag

Kvotientregelen

Så ser vi på hvordan vi deriverer en kvotient av to funksjoner:

$\fbox{$\bigg( \frac{\displaystyle f(x)}{\displaystyle g(x)} \bigg)′ = \frac{\displaystyle f′(x)\cdot g(x) − f(x) \cdot g′(x)}{\displaystyle \big(g(x)\big)^2}$}$

På kortform:

$\fbox{$\Big( \frac{\displaystyle u}{\displaystyle v} \Big)′ = \frac{\displaystyle u′v − uv′}{\displaystyle v^2} $}$

Vi deriverer altså en brøk ved å kvadrere nevneren, og sette telleren lik den deriverte av telleren multiplisert med nevneren, minus telleren multiplisert med den deriverte av nevneren.

Kvotientregelen kalles ofte brøkregelen.

Eksempel 6:

$\Big( \frac{\displaystyle x}{\displaystyle \ln x} \Big)′ = \frac{\displaystyle x′ \cdot \ln x − x \cdot (\ln x)′}{\displaystyle (\ln x)^2} = \frac{\displaystyle 1 \cdot \ln x − x \cdot \frac{1}{x}}{\displaystyle (\ln x)^2} = \frac{\displaystyle \ln x − 1}{\displaystyle (\ln x)^2}$

Eksempel 7:

Ved å benytte at $\tan x = \frac{\displaystyle \sin x}{\displaystyle \cos x}$, kan vi bruke kvotientregelen til å finne den deriverte til tan x:

$(\tan x)′ = \big( \frac{\displaystyle \sin x}{\displaystyle \cos x} \big)′ = \frac{\displaystyle (\sin x)′ \cdot \cos x − \sin x \cdot (\cos x)′}{\displaystyle \cos^2 x} =$

$\frac{\displaystyle \cos x \cdot \cos x − \sin x \cdot (−\sin x)}{\displaystyle \cos^2 x} = \frac{\displaystyle \cos^2 x + \sin^2 x}{\displaystyle \cos^2 x}$

Nå kan vi bruke identiteten cos² x + sin² x = 1 til å regne svaret om slik:

$\frac{\displaystyle \cos^2 x + \sin^2 x}{\displaystyle \cos^2 x} = \frac{\displaystyle 1}{\displaystyle \cos^2 x} = \sec^2 x$

Eller vi kan regne slik

$\frac{\displaystyle \cos^2 x + \sin^2 x}{\displaystyle \cos^2 x} = \frac{\displaystyle \cos^2 x}{\displaystyle \cos^2 x} + \frac{\displaystyle \sin^2 x}{\displaystyle \cos^2 x} = 1 + \tan^2 x$

Dette er formene til den deriverte av tangens som vi presenterer i artikkelen om å derivere ulike typer funksjoner.

Kvotientregelen gir oss også en metode til å derivere rasjonale funksjoner. Rasjonale funksjoner er deriverbare for alle x unntatt de som gjør at nevneren blir 0.

Oppgave 3:

Deriver funksjonen $f(x) = \frac{\displaystyle x^2 + 1}{\displaystyle x + 1}$

Se løsningsforslag

Hvis vi har en rasjonal funksjon der telleren er en konstant og nevneren en potensfunksjon, kan det gjerne være enklere å derivere ved hjelp av potensregelen enn ved hjelp av kvotientregelen.

Eksempel 8:

Vi skal derivere funksjonen $f(x) = \frac{\displaystyle 2}{\displaystyle 3x^2}$

Vi bruker potensregelen:

$f′(x) = \Big(\frac{\displaystyle 2}{\displaystyle 3}x^{−2}\Big)′ = \frac{\displaystyle 2}{\displaystyle 3} \cdot (−2)x^{−3} = −\frac{\displaystyle 4}{\displaystyle 3x^3}$

Vi bruker kvotientregelen:

$f′(x) = \frac{\displaystyle 2′ \cdot 3x^2 − 2 \cdot (3x^2)′}{\displaystyle \big(3x^2\big)^2} = \frac{\displaystyle 0 \cdot 3x^2 − 2 \cdot 3 \cdot 2x}{\displaystyle 9x^4} = −\frac{\displaystyle 12x}{\displaystyle 9x^4} = −\frac{\displaystyle 4}{\displaystyle 3x^3}$

Oppgave 4:

Deriver funksjonen $f(x) = \frac{\displaystyle 3}{\displaystyle 2x}$ både ved å bruke potensregelen og ved å bruke kvotientregelen.

Se løsningsforslag

Kjerneregelen

Den siste regelen vi skal se på, er kjerneregelen, som vi bruker når vi skal derivere sammensatte funksjoner.

$\fbox{ $\Big(f\big(g(x)\big)\Big)′ = f′(g) \cdot g′(x)$}$

På kortform:

$\fbox{ $\big(u(v)\big)′ = u_{\large v^\phantom 1}′v′$}$

Her deriveres u med hensyn på v som uavhengig variabel og v med hensyn på sin egen uavhengige variabel.

Kjerneregelen sier altså at hvis en funksjon består av en ytre funksjon, f(g), og en indre funksjon, g(x), beregner vi den deriverte ved å multiplisere den deriverte av den ytre funksjonen med hensyn på g med den deriverte av den indre funksjonen med hensyn på x.

Eksempel på en sammensatt funksjon er f(x) = e^2x, som er sammensatt av funksjonene f(g) = e^g og g(x) = 2x.

For å kunne bruke kjerneregelen, må vi først finne kjernen. En strategi til dette er å lete etter et uttrykk som, hvis vi erstatter det med en enkelt variabel, gir oss en funksjon vi har en regel for å derivere.

Et par eksempler vil klargjøre:

Eksempel 9:

Vi skal derivere f(x) = e^2x.

Vi ser at hvis vi erstatter 2x med g, får vi e^g, som vi vet hvordan vi deriverer. Den eneste forskjellen i forhold til det vi har gjort tidligere, er at variabelen heter g, ikke x, så (e^g)′ = e^g.

Vi har altså at den ytre funksjonen er f(g) = e^g og den indre funksjonen er g(x) = 2x.

Kjerneregelen gir

f′(x) = (e^2x)′ = (e^g)′ · (2x)′ = e^g · 2.

Så gjenstår det bare å erstatte tilbake g med 2x, så vi får e^2x · 2 = 2e^2x.

Altså:

(e^2x)′ = 2e^2x

Eksempel 10:

Vi skal derivere $f(x) = \sqrt {\ln x}$

Vi ser at hvis vi erstatter ln x med g, får vi $\sqrt g$, som vi vet hvordan vi deriverer. Og vi får:

$f′(x) = (\sqrt g)′ \cdot (\ln x)′ = \frac{\displaystyle 1}{\displaystyle 2 \sqrt g} \cdot \frac{\displaystyle 1}{\displaystyle x} = \frac{\displaystyle 1}{\displaystyle 2x\sqrt{ \ln x }}$

På engelsk heter kjerneregelen the chain rule, kjederegelen. Vi ser at det er et dekkende navn fordi vi utfører en kjede av derivasjoner. Dette blir enda tydeligere hvis vi har flere kjerner inni hverandre.

Oppgave 5:

Deriver funksjonen f(x) = ln(4x + 8).

Se løsningsforslag

Oppgave 6:

Deriver funksjonen $f(x) = e^{(x^{\large 2})}$.

Se løsningsforslag

Hvis vi er usikre på om vi trenger å bruke kjerneregelen eller ikke, er det bedre å bruke den en gang for mye enn en gang for lite. Bruker vi kjerneregelen der det egentlig ikke er behov for det, skjer det ikke noe annet enn at den deriverte av kjernen blir 1, slik som vist i eksempel 11:

Eksempel 11:

Vi skal derivere f(x) = e^x⁺².

Vi har at den ytre funksjonen er f(g) = e^g og den indre funksjonen er g(x) = x + 2.

Kjerneregelen gir f′(x) = (e^x⁺²)′ = (e^g)′ · (x + 2)′ = (e^g) · 1 = e^x⁺².

Den deriverte av kjernen markert med oransje. Vi ser at den er 1, så det var ikke nødvendig å bruke kjerneregelen her.

Kilder

- Gulliksen, T. & Hole, A. (2010). Matematikk i praksis. Universitetsforlaget
- Thomas, G.B., Finney R.L. (1988). Calculus and Analytic Geometry. Addison-Wesley.
- matematikk.org

27. februar 201821. januar 2025

Derivere ulike typer funksjoner

I artikkelen om å derivere potensfunksjoner lærer vi å derivere potensfunksjoner. Her skal vi kjapt presentere derivasjonsregler for noen andre typer funksjoner.

Trigonometriske funksjoner

$\fbox{$\begin{align}(\sin x)′ &= \cos x \\
(\cos x)′ &= −\sin x \end{align}$}$

Den deriverte av sinus er altså cosinus, og den deriverte av cosinus er minus sinus.

Sinus- og cosinusfunksjoner er deriverbare for alle x.

Det finnes flere vanlige formater å presentere den deriverte av tangens på:

$\fbox{$\begin{align}(\tan x)′ &= \frac{\displaystyle 1}{\displaystyle \cos^2 x} \\
&\, \\
(\tan x)′ &= \sec^2 x \\
&\, \\
(\tan x)′ &= 1 + \tan^2x\end{align}$}$

Tangensfunksjonen er deriverbar der den er definert, det vil si for alle x unntatt x = 90° + n · 180°.

Eksponentialfunksjoner

$\fbox{ $(a^x)′ = a^x \ln a$}$

Vi deriverer altså en eksponentialfunksjon ved å la funksjonen stå, og multiplisere med den naturlige logaritmen til vekstfaktoren.

Eksempel 1:

Vi har f(x) = 3^x og skal finne den deriverte. Vi bruker regelen for derivasjon av eksponentialfunksjoner og får f′(x) = 3^x ln 3.

Eksempel 2:

Vi har f(x) = e^x og skal finne den deriverte. Vi bruker regelen for derivasjon av eksponentialfunksjoner og får f′(x) = e^x ln e = e^x · 1 = e^x.

Eksempel 2 viser et spesialtilfelle av regelen for derivasjon av eksponentialfunksjoner, der vekstfaktoren er e. Denne funksjonen, som brukes mye, er sin egen deriverte. Vi har altså

$\fbox{$(e^x)′ = e^x$}$

Eksponentialfunksjoner er deriverbare for alle x.

Oppgave 1:

Deriver funksjonen f(x) = 12^x.

Se løsningsforslag

Logaritmefunksjoner

$\fbox{$(\log_ax)′ =\frac{\displaystyle 1}{\displaystyle x \ln a}$}$

Vi deriverer altså en logaritmefunksjon ved å multiplisere variabelen med den naturlige logaritmen til funksjonens grunntall, og sette produktet under brøkstrek.

Eksempel 3:

Vi har f(x) = log₁₀x og skal finne den deriverte. Vi bruker regelen for derivasjon av logaritmefunksjoner og får $(\log_{10}x)′ = \frac{\displaystyle 1}{\displaystyle x \ln 10}$

Eksempel 4:

Vi har f(x) = ln x og skal finne den deriverte. Vi bruker regelen for derivasjon av logaritmefunksjoner og får $(\ln x)′ = \frac{\displaystyle 1}{\displaystyle x \ln e} = \frac{\displaystyle 1}{\displaystyle x \cdot 1} = \frac{\displaystyle 1}{\displaystyle x}$

Eksempel 4 viser et spesialtilfelle av regelen for derivasjon av logaritmefunksjoner, der grunntallet er e. Denne funksjonen, som brukes mye, har altså den inverse av variabelen som derivert.

$\fbox{$(\ln x)′ = \frac{\displaystyle 1}{\displaystyle x}$}$

Logaritmefunksjoner er deriverbare for alle x i definisjonsområdet, det vil si alle x som er større enn 0.

Oppgave 2:

Deriver funksjonen f(x) = log₂x.

Se løsningsforslag

Gjentatte potensderivasjoner

I artikkelen om å derivere potensfunksjoner ser vi at vi subtraherer 1 i eksponenten når vi deriverer en potensfunksjon. Starter vi med et naturlig tall, n, i eksponenten og deriverer gjentatte ganger, får vi derfor en kjede av stadig lavere potenser inntil vi når 0:

xⁿ → xⁿ^{− 1} → … → x² → x → 1 → 0

Vi kommer ikke forbi 0.

Men siden $\frac{\displaystyle 1}{\displaystyle x}$ kan skrives som $x^{−1}$ og $(\ln x)′ =\frac{\displaystyle 1}{\displaystyle x}$, ser vi at vi med ln x kan starte en ny kjede med negative eksponenter:

ln x → x⁻¹ → x⁻² → x⁻³ → …

Kilder

- Gulliksen, T. & Hole, A. (2010). Matematikk i praksis. Universitetsforlaget
- Thomas, G.B., Finney R.L. (1988). Calculus and Analytic Geometry. Addison-Wesley.
- matematikk.org

27. februar 201821. januar 2025

Derivere potensfunksjoner

Potensfunksjoner generelt

I artikkelen om derivasjonsbegrepet ser vi at (x²)′ = 2x. To-tallet i eksponenten har kommet ned, og står som en koeffisient foran x. Dette er et spesialtilfelle av en regel som sier at vi for alle eksponenter, r, har følgende sammenheng:

$\fbox{Derivasjon av potens: $(x^r)′ = r x^{r−1}$}$

Vi deriverer altså en potens ved å flytte ned eksponenten og så redusere den med 1.

Eksempel 1:

(x⁸)′ = 8x⁷

Førstegradsfunksjoner

Potensregelen gjelder også for r = 1:

Eksempel 2:

x′ = (x¹)′ = 1x⁰ = 1. Den deriverte av x er altså 1. Dette er logisk, for 1 er jo nettopp stigningstallet til grafen til f(x) = x.

Konstantfunksjoner

Potensregelen gjelder også for r = 0:

Eksempel 3:

(x⁰)′ = 0x⁻¹ = 0. Dette er logisk, for x⁰ = 1, og grafen til f(x) = 1 er ei horisontal linje. Funksjonen har aldri noen endring i verdi, og den deriverte er følgelig 0.

Ingen konstantfunksjoner, f(x) = k, har noen endring i funksjonsverdi, og vi har for alle konstanter, k, at den deriverte er 0.

$\fbox{Derivasjon av konstant: $k′ = 0$}$

Variabel under brøkstrek

Potensregelen gjelder også for negative r, så vi kan benytte at $\frac{\displaystyle 1}{\displaystyle x^r} = x^{−r} $ til å derivere uttrykk der variabelen står under en brøkstrek:

Eksempel 4:

${\Large (\frac{1}{x^2})}′ = (x^{−2})′ = −2 x^{−3} = −{\Large \frac{2}{x^3}}$

Eksempel 5:

${\Large (\frac{1}{x})}′ = (x^{−1})′ = −1 x^{−2} = −{\Large \frac{1}{x^2}}$

Invers

Resultatet fra eksempel 5 kan være verd å huske som en egen regel:

$\fbox{Derivasjon av invers:${\Large (\frac{1}{x})}′ = −{\Large \frac{1}{x^2}}$}$

Rotuttrykk

Potensregelen gjelder også for r som ikke er hele tall, så vi kan benytte at $\sqrt[\LARGE n]{x} = x^{\Large \frac{1}{n}}$ til å derivere rotuttrykk:

Eksempel 6:

$\sqrt{x}$ betyr egentlig $\sqrt[\Large 2]{x}$, så

$(\sqrt x)′ = (x^{\large \frac{1}{2}})′ = {\large \frac{1}{2}}x^{−\large \frac{1}{2}} = \frac{\displaystyle 1}{\displaystyle 2x^{\large \frac{1}{2}}} =\frac{\displaystyle 1}{\displaystyle 2\sqrt x}$

Resultatet fra eksempel 6 kan være verd å huske som en egen regel:

$\fbox{Derivasjon av kvadratrot:$\big(\sqrt x \big)′ = \frac{\displaystyle 1}{\displaystyle 2\sqrt x}$}$

Eksempel 7:

$(\sqrt[\Large 3] x)′ = (x^{\large \frac{1}{3}})′ = {\large \frac{1}{3}}x^{−\large \frac{2}{3}} = \frac{\displaystyle 1}{\displaystyle 3x^{\large \frac{2}{3}}} =\frac{\displaystyle 1}{\displaystyle 3\sqrt[\Large 3] {x^2}}$

Potensfunksjoner er deriverbare for alle x.

Oppgave 1:

Bruk potensregelen til å derivere følgende funksjoner:

$f(x) = x^5$
$f(x) = {\Large \frac{1}{x^4}}$
$f(x) = {\Large \frac{1}{\sqrt x}}$

Se løsningsforslag

Kilder

- Gulliksen, T. & Hole, A. (2010). Matematikk i praksis. Universitetsforlaget
- Thomas, G.B., Finney R.L. (1988). Calculus and Analytic Geometry. Addison-Wesley.
- matematikk.org

23. februar 201821. januar 2025

Derivasjonsbegrepet

Illustrasjon av derivasjon

Vi har en plante som i en periode vokser kjapt, med konstant hastighet. Den er i utgangspunktet 1 desimeter høy. Etter en uke er den 3 desimeter, og etter 2 uker 5 desimeter. Så skal vi regne ut vekstfarten i denne perioden. Og det er jo lett, vi tar bare høyden en uke og trekker fra høyden uka før. For eksempel 3 − 1 = 2, eller 5 − 3 = 2. Eller vi kan måle endringen over 2 uker og dele på to: (5 − 1)/2 = 2. Vekstfarten er 2 desimeter pr. uke.

En funksjon som beskriver plantens høyde vil være f(x) = 2x + 1, der x er antall uker, med graf som vist under.

Graf som viser lineær vekst av plante

Vi kan finne vekstfarten ved å velge to hvilke som helst verdier av x, la oss kalle dem x₁ og x₂, og regne ut

$\frac{\displaystyle f(x_2) − f(x_1)}{\displaystyle x^{\phantom 1}_2 − x_1}$

for eksempel

${\large \frac{f(2) − f(0)}{2 − 0}} = {\large \frac{5−1}{2 − 0}} =2$

Vi gjenkjenner dette som grafens stigningstall, som er 2 for alle x.

Men la oss nå si at vi i stedet si har en eksponentialfunksjon som angir antall bakterier en kultur, f(x) = 1,35^x.

Grafen til funksjonen er vist under, enheten langs x-aksen er timer, enheten langs y-aksen millioner bakterier:

Graf som viser eksponentiell vekst i en bakteriekultur

Her er ikke stigningstallet konstant, noe som betyr at vekstfarten endrer seg. Måler vi mellom to punkter, vil vekstfarten avhenge av hvilke punkter vi velger, den vil ikke være konstant, slik som med planten.

Velger vi å måle mellom 0 og 1 time, får vi

${\large\frac{f(1) − f(0)}{1 − 0}} = {\large\frac{1{,}35^1 − 1{,}35^0}{1 − 0}} = 0{,}35$

Gjennomsnittlig vekstfart den første timen er altså 350 000 bakterier per time.

Velger vi å måle mellom 1 og 2 timer, får vi

${\large\frac{f(2) − f(1)}{2 − 1}} = {\large\frac{1{,}35^2 − 1{,}35^1}{2 − 1}} = 0{,}4725$

Gjennomsnittlig vekstfart den andre timen er altså 472 500 bakterier per time.

Dette er gjennomsnittlige vekstfarter målt i løpet av en time. Men så lurer vi på hva vekstfarten er i et gitt øyeblikk, for eksempel etter nøyaktig 1,5 timer. Vi kan finne en tilnærming ved å beregne gjennomsnittet i et intervall rundt 1,5 timer, for eksempel fra 1,3 til 1,7:

${\large\frac{f(1{,}7) − f(1{,}3)}{1{,}7 − 1{,}3}} = {\large\frac{1{,}35^{1{,}7} − 1{,}35^{1{,}3}}{1{,}7 − 1{,}3}} \approx 0{,}471014$

Om lag 471 014 bakterier per time.

Vil vi ha et mer nøyaktig anslag, kan vi bruke et smalere intervall, for eksempel fra 1,4 til 1,6:

${\large\frac{f(1{,}6) − f(1{,}4)}{1{,}6 − 1{,}4}} = {\large\frac{1{,}35^{1{,}6} − 1{,}35^{1{,}4}}{1{,}6 − 1{,}4}} \approx 0{,}470802$

Om lag 470 802 bakterier per time.

Vi kan finne bedre og bedre tilnærminger ved å velge smalere og smalere intervaller, men noen helt eksakt verdi vil vi aldri klare å finne. Her kommer den deriverte oss til hjelp. Den deriverte er en ny funksjon som forteller oss hvor fort den opprinnelige funksjonen endrer seg. Som vi senere skal lære å regne ut, blir den deriverte av bakteriefunksjonen

f′(x) = ln 1,35 · 1,35^x

Apostrofen i f′(x) forteller oss at denne funksjonen er den deriverte av funksjonen f(x).

Setter vi inn x = 1,5, finner vi vekstfarten ved nøyaktig 1,5 timer:

f′(1,5) = ln 1,35 · 1,35^1,5 ≈ 0,470732

Om lag 470 732 bakterier per time.

Definisjon av den deriverte

For å finne et uttrykk for den deriverte til en funksjon, gjør vi som i eksemplet over, ser på smalere og smalere intervaller. Det kan være litt krevende å henge med i logikken her, men den er nødvendig for å forstå hva den deriverte er. Senere skal vi etablere regler for derivasjon som er enkle å bruke.

Vi tar utgangspunkt i en vilkårlig funksjon, f(x), og velger to vilkårlige x-verdier. Nå kaller vi dem imidlertid ikke x₁ og x₂, men x og x + Δx. Det er for å indikere at vi velger et vilkårlig punkt, x, og går en vilkårlig avstand til høyre fra x for å finne det andre punktet. Δx betyr en ikke nærmere bestemt avstand. I disse to punktene leser vi så av funksjonsverdiene, f(x) og f(x + Δx), som illustrert under:

Illustrasjon av definisjon av den deriverte

Den gjennomsnittlige endringsfarten mellom x og x + Δx blir

${\large\frac{f(x + \Delta x ) − f(x)}{(x+ \Delta x) − x }} = {\large\frac{f(x + \Delta x ) − f(x)}{ \Delta x}}$

For å finne endringsfarten akkurat i x, reduserer vi Δx, slik at punktet x + Δx nærmer seg x. Jo mindre Δx blir, jo nærmere den riktige verdien kommer vi. Den helt eksakte verdien er grensen for uttrykket over finner vi når vi lar Δx gå mot null.

Grenser blir vi kjent med i artikkelen om kontinuitet og grenser, der vi også lærer å uttrykke grenser ved hjelp av lim-terminologi. Her skal vi altså finne

$\fbox{$ \displaystyle \lim_{\Delta x \to 0} \frac{f(x + \Delta x ) − f(x)}{ \Delta x}$}$

Denne grensen er selve definisjonen av den deriverte, f′, av funksjonen f, som altså forteller hvor fort f endrer seg for en vilkårlig x.

Eksempel 1:

Vi skal bruke definisjonen av den deriverte til å finne f′(x) når f(x) = x².

Vi får

$f′(x) = \displaystyle \lim_{\Delta x \to 0} \frac{f(x + \Delta x ) − f(x)}{ \Delta x} = \displaystyle \lim_{\Delta x \to 0} \frac{(x + \Delta x)^2 − x^2}{ \Delta x} =$

$\displaystyle \lim_{\Delta x \to 0} \frac{x^2 + 2x \Delta x +(\Delta x)^2 − x^2}{ \Delta x} = \displaystyle \lim_{\Delta x \to 0} \frac{2x \Delta x +(\Delta x)^2}{ \Delta x} =$

$\displaystyle \lim_{\Delta x \to 0} 2x + \Delta x = 2x$

Vi har altså at (x²)′ = 2x.

Det ble en ganske lang utregning, men det er bare vanlig algebra som er brukt. Vi setter først inn funksjonsuttrykket, der f(x + Δx) er (x + Δx)² og f(x) er x². Så bruker vi første kvadratsetning, trekker sammen like ledd, og forkorter med Δx. Til slutt regner vi ut grenseverdien når Δx → 0.

Oppgave 1:

Bruk definisjonen av den deriverte til å finne f′(x) når f(x) = 2x + 3.

Se løsningsforslag

Deriverbarhet

Det er ikke alle funksjoner som er deriverbare i alle områder. For at en funksjon skal være deriverbar i et område, må den være kontinuerlig, og grafen uten knekkpunkter.

Eksempel 2:

Vi ser på funksjonen $f(x) = \frac{\displaystyle|x|}{\displaystyle x}$, som vi møtte i avsnitt 1 og som har en graf som vist under.

En diskontinuerlig graf

Når x < 0, er funksjonen kontinuerlig og glatt, og derfor deriverbar. Samme argument gjelder for x > 0. Men akkurat i x = 0 hopper funksjonsverdien fra −1 til 1 og det er meningsløst å snakke om en endringshastighet. Funksjonen er ikke deriverbar for x = 0.

Eksempel 3:

Vi ser på funksjonen f(x) = |x|, som har en graf som vist under.

En graf med knekk

Det er ingen problemer med funksjonens grenseverdier i x = 0, den høyresidige og venstresidige grenseverdien er lik funksjonsverdien, $\displaystyle \lim_{x \to 0^{\large +}}f(x) = \displaystyle \lim_{x \to 0^{\large −}}f(x) = f(0) = 0$, så funksjonen er kontinuerlig.

Den har imidlertid et knekkpunkt. Når x < 0, har vi at f(x) = −x, og når x > 0, har vi at f(x) = x. Ser vi på definisjonen av den deriverte i x = 0, vil vi ha at

$\displaystyle \lim_{\Delta x \to 0^{\Large +}} \frac{f(0 + \Delta x ) − f(0)}{ \Delta x} = \displaystyle \lim_{\Delta x \to 0^{\Large +}} \frac{(0 + \Delta x ) − 0}{ \Delta x} = 1$

$\displaystyle \lim_{\Delta x \to 0^{\Large −}} \frac{f(0 + \Delta x ) − f(0)}{ \Delta x} = \displaystyle \lim_{\Delta x \to 0^{\Large −}} \frac{−(0 + \Delta x ) − 0}{ \Delta x} = −1$

Den høyresidige og venstresidige grenseverdien er ikke lik, så grenseverdien, og derved den deriverte, er ikke definert i x = 0.

Dette er intuitivt riktig, den deriverte representerer funksjonens endringshastighet, og det finnes ingen fast endringshastighet i et punkt der grafen knekker.

Vi kan godt si at en funksjon ikke er deriverbar i et punkt hvis vi ikke kan tegne en entydig tangent til grafen i punktet. I eksempel 3 for eksempel, kan vi jo ikke tegne en entydig tangent i x = 0.

Kilder

- Gulliksen, T. & Hole, A. (2010). Matematikk i praksis. Universitetsforlaget
- Thomas, G.B., Finney R.L. (1988). Calculus and Analytic Geometry. Addison-Wesley.
- matematikk.org

1. juni 201716. januar 2025

Asymptoter

Horisontale asymptoter

Under vises grafen til funksjonen $f(x) = 1 + \frac{\displaystyle 2}{\displaystyle x^2 + 1}$.

Vi ser at mot høyre og venstre, altså når x går mot ∞ eller −∞, nærmer grafen seg den stiplede grønne linja som ligger i y = 1.

Horisontal asymptote i y = 1

Hvis grafen til en funksjon nærmer seg ei horisontal linje når variabelen går mot ∞ eller −∞, er denne linja en horisontal asymptote til funksjonen.

Hvis vi i f(x) over setter inn x = 10, får vi

$f(x) = 1 + {\large \frac{2}{10^2 + 1}} = 1 + {\large \frac{2}{101}} \approx 1{,}02$

Setter vi inn x = 100, får vi

$f(x) = 1 + {\large \frac{2}{100^2 + 1}} = 1 + {\large \frac{2}{10 \, 001}} \approx 1{,}0002$

Setter vi inn x = 1000, får vi

$f(x) = 1 + {\large \frac{2}{1000^2 + 1}} = 1 + {\large \frac{2}{1\, 000 \, 001}} \approx 1{,}000002$

Jo høyere x-verdier vi setter inn, jo nærmere kommer grafen til linja y = 1. Vi kan komme så nærme vi bare vil, ved å sette inn store nok verdier, men vi vil aldri komme helt borttil.

For å finne ut om en funksjon har en horisontal asymptote, undersøker vi hva som skjer når variabelen går mot ∞ eller −∞. Hvis funksjonsforskriften da går mot et konstantuttrykk, har vi en horisontal asymptote.

At noe går mot uendelig eller minus uendelig, skriver vi gjerne slik: → ±∞.

I GeoGebra kan vi finne asymptoter ved hjelp av kommandoen asymptote.

Eksempel 1:

Vi skal avgjøre om funksjonen $f(x) = −2 + \frac{\displaystyle 5}{\displaystyle x^2 + 3}$ har en horisontal asymptote, og sjekke svaret i GeoGebra.

Når x → ±∞, går nevneren i brøken mot uendelig, noe som betyr at brøken går mot 0, og vi står igjen med f(x) = −2. Funksjonsforskriften går mot konstanten −2, så y = −2 er en horisontal asymptote for f(x).

I GeoGebra skriver vi først -2 + 5/(x^2 + 3) i inntastingsfeltet. Deretter skriver vi asymptote(f). GeoGebra angir funksjonsforskriften for ei linje i y = −2 i algebrafeltet, og tegner asymptoten i grafikkfeltet.

Et plott av grafen og asymptoten er vist under.

Horisontal asymptote i y = -2

Oppgave 1:

Avgjør om funksjonen $f(x) = \frac{\displaystyle 1}{\displaystyle x^2 + 1}$ har en horisontal asymptote, og sjekk svaret i GeoGebra.

Se løsningsforslag

Skråasymptoter

Hvis funksjonsforskriften går mot et konstantuttrykk når variabelen går mot ±∞, har vi altså en horisontal asymptote. Hvis den i stedet går mot en førstegradsuttrykk, har vi en skråasymptote.

Eksempel 2:

Vi har funksjonen $f(x) = x + 2 + \frac{\displaystyle 7}{\displaystyle x^2 + 1}$.

Når x → ±∞, går nevneren i brøken mot uendelig, noe som betyr at brøken går mot 0, og vi står igjen med f(x) = x + 2.
Funksjonsforskriften går mot førstegradsuttrykket x + 2, så y = x + 2 er en skråasymptote for f(x).

Et plott av grafen og asymptoten er vist under.

Skråasymptote i y = x + 2

I spesielle tilfeller kan en funksjon ha både en horisontal asymptote og en skråasymptote. En skråasymptote når x → ∞ og en horisontal asymptote når x → −∞, eller omvendt. Et eksempel er vist under, i grafen til $f(x) = x + \sqrt{x^2 + 4}$. Her har vi en skråasymptote y = 2x når x → ∞, og en horisontal asymptote y = 0 når x → −∞.

Skråasymptote når x → ∞ og hotisontal asymptote når x → −∞

Vertikale asymptoter

Horisontale asymptoter og skråasymptoter er altså henholdsvis vannrette og skrå linjer som grafen nærmer seg når variabelen går mot ±∞.

Vertikale asymptoter er loddrette linjer som grafen nærmer seg i punkter der funksjonsverdien går mot uendelig.

Eksempel 3:

Vi har funksjonen $f(x) = x^2 + \frac{\displaystyle 2}{\displaystyle x − 1}$.

Når x → 1, går nevneren i brøken mot 0, så brøken går mot uendelig. Grafen vil derfor legge seg inntil linja x = 1, og x = 1 er en vertikal asymptote for f(x).

Et plott av grafen og asymptoten er vist under.

Vertikal asymptote i x = 1

Vertikale asymptoter er altså variabelverdier der funksjonsverdien går mot uendelig.

Blanding av asymptoter

Det kan godt være at en funksjon har vertikale asymptoter samtidig som den har horisontale asymptoter eller skråasymptoter.

Eksempel 4:

Vi har funksjonen $f(x) = x + \frac{\displaystyle 2}{\displaystyle x − 3}$.

Når x → ±∞, går nevneren i brøken mot uendelig, noe som betyr at brøken går mot 0, og vi står igjen med f(x) = x.
Så y = x er en skråasymptote for f(x).

Når x → 3, går nevneren i brøken mot 0, så brøken går mot uendelig. Grafen vil derfor legge seg inntil linja x = 3, og x = 3 er en vertikal asymptote for f(x).

Et plott av grafen og asymptotene er vist under.

Skråasymptote i y = x og vertikal asymptote i x = 3

Oppgave 2:

Avgjør om funksjonen $f(x) = 1 + \frac{\displaystyle 2}{\displaystyle x^2 − 4}$ har asymptoter, og sjekk svaret i GeoGebra.

Se løsningsforslag

Funksjonstyper med asymptoter

Alle funksjonene vi har arbeidet med så langt, kan skrives om til rasjonale funksjoner.

Eksempel 5:

Vi kan skrive $f(x) = −2 + \frac{\displaystyle 5}{\displaystyle x^2 + 3}$ fra eksempel 1 som en rasjonal funksjon ved å multiplisere −2 med $\frac{\displaystyle x^2 + 3}{\displaystyle x^2 + 3}$ og sette på felles brøkstrek:

$f(x) = −2 \cdot \frac{\displaystyle x^2 + 3}{\displaystyle x^2 + 3} + \frac{\displaystyle 5}{\displaystyle x^2 + 3} = \frac{\displaystyle −2x^2 − 6}{\displaystyle x^2 + 3} + \frac{\displaystyle 5}{\displaystyle x^2 + 3} = \frac{\displaystyle −2x^2 − 6 + 5}{\displaystyle x^2 + 3} = \frac{\displaystyle −2x^2 − 1}{\displaystyle x^2 + 3} $

Grunnen til at vi ikke har skrevet funksjonene på denne formen tidligere, er at det da er vanskeligere å finne asymptotene.

I en rasjonal funksjon vil vi ha:

- En horisontal asymptote hvis polynomene i teller og nevner har samme grad.
- En horisontal asymptote i 0 hvis polynomet i teller har lavere grad enn polynomet i nevner.
- En skråasymptote hvis graden til polynomet i teller er 1 høyere enn graden til polynomet i nevner.
- Ingen asymptote hvis polynomet i teller er mer enn 1 grad høyere enn polynomet i nevner.

Ofte vil det være i rasjonale funksjoner vi finner asymptoter, men også andre funksjonstyper har asymptoter. Logaritmefunksjoner har for eksempel en vertikal asymptote i x = 0, fordi funksjonsverdien går mot minus uendelig når x går mot 0. f(x) = tan(x) har uendelig mange vertikale asymptoter i $x = {\large \frac{(2k + 1)\pi}{2}}$, der k er et vilkårlig helt tall, slik det er illustrert under.

Asymptoter til tangens

GeoGebra klarer imidlertid ikke å finne asymptotene til tangensfunksjoner.

Polynomfunksjoner har ikke asymptoter. De går ikke mot noe konstant- eller førstegradsuttrykk når variabelen går mot uendelig, og det finnes heller ingen variabelverdier der funksjonsverdien går mot uendelig.

Ubestemte uttrykk

I brøkene i eksempler og oppgaver har vi så langt hatt tellere som har vært konstanter, for eksempel 1 og 2. Vi har derfor kunnet konkludere med at hvis nevneren går mot 0, går brøken mot uendelig, og hvis nevneren går mot uendelig, går brøken mot 0. Hvis telleren ikke er en konstant, er det imidlertid ikke sikkert at det vil være slik, for det kan være at både teller og nevner går mot 0 eller uendelig samtidig. Vi får da et ubestemt uttrykk vi ikke umiddelbart kan se om går mot en asymptote.

Eksempel 6:

Vi har $f(x) = \frac{\displaystyle −2x^2 − 1}{\displaystyle x^2 + 3}$. Når x → ±∞, går både teller og nevner mot uendelig.

Vi kan ikke direkte finne noen asymptoter til funksjonen i eksempel 6. Men det er en rasjonal funksjon med polynomer av samme grad i teller og nevner, så vi vet vi at den har en horisontal asymptote. For å finne den horisontale asymptoten i en rasjonal funksjon med samme grad i teller og nevner, kan vi dividere alle ledd i teller og nevner med høyeste grad av variabelen. Ledd av høyeste grad vil da bli redusert til sine koeffisienter, og andre ledd vil gå mot 0 når x → ±∞.

Eksempel 7:

Vi har $f(x) = \frac{\displaystyle −2x^2 − 1}{\displaystyle x^2 + 3}$, som i eksempel 6. Høyeste potens av x er 2, så vi dividerer alle ledd med x²:

$f(x) = \frac{\displaystyle −2x^2 − 1}{\displaystyle x^2 + 3 } = \frac{\displaystyle \frac{−2x^2}{x^2} − \frac{1}{x^2 }}{\displaystyle \frac{x^2}{x^2} + \frac{3}{x^2 }} = \frac{\displaystyle −2 − \frac{1}{x^2 }}{\displaystyle 1 + \frac{3}{x^2 }}$

Vi ser at −2x² blir redusert til koeffisienten −2, og x² blir redusert til koeffisienten 1. Når x → ±∞, går delbrøkene ${\large \frac{1}{x^2}}$ og ${\large \frac{3}{x^2}}$ mot 0, så vi står igjen med $f(x) = {\large \frac{−2}{1}} = −2$.

Så y = −2 er en horisontal asymptote for f(x).

Oppgave 3:

Finn den horisontale asymptoten til $f(x) = \frac{\displaystyle x^3 + 6x}{\displaystyle 3x^3 + x^2 + 1}$.

Se løsningsforslag

Oppgave 4:

I en matematisk modell for forurensing i en innsjø er forskere kommet fram til at giftmengden, målt i g/m³, ved t døgn er gitt ved $f(t) = {\large \frac{10t^2}{4t^2+6t+9}}$. De konkluderer da med at giftmengden i det lange løp vil stabilisere seg på 2,5 g/m³. Hvordan kommer de fram til dette?

Se løsningsforslag

Oppgave 5:

Finn eventuelle horisontale og vertikale asymptoter til funksjonen

$f(x) = \frac{\displaystyle −x^2 + x − 2}{\displaystyle x^2 − 1}$

Skjermfilm Se film med løsningsforslag

En rasjonal funksjon der graden til polynomet i teller er 1 høyere enn graden til polynomet i nevner, vet vi har en skråasymptote. Men hvis både teller og nevner går mot uendelig når x → ±∞, hjelper det ikke å dividere alle ledd i teller og nevner med høyeste grad av variabelen. Da vil vi få en konstant i teller og et uttrykk som går mot 0, i nevner.

Eksempel 8:

Vi skal finne skråasymptoten til $f(x) = \frac{\displaystyle x^3 + 2}{\displaystyle x^2 + 1}$.

Høyeste potens av x er 3, så vi dividerer alle ledd med x³:

$f(x) = \frac{\displaystyle x^3 + 2}{\displaystyle x^2 + 1} = \frac{\displaystyle \frac{x^3}{x^3} + \frac{2}{x^3}}{\displaystyle \frac{x^2}{x^3} + \frac{1}{x^3}} = \frac{\displaystyle 1 + \frac{2}{x^3}}{\displaystyle \frac{1}{x} + \frac{1}{x^3}}$

Delbrøkene går mot 0 når x → ±∞, så vi får 1 i teller og 0 i nevner. Vi kan da bare konkludere med at brøken går mot uendelig, men ikke si noe om skråasymptoten.

I tilfeller der graden til polynomet i teller er 1 høyere enn graden til polynomet i nevner, kan vi i stedet utføre en polynomdivisjon.

Eksempel 9:

Vi har $f(x) = \frac{\displaystyle x^3 + 2}{\displaystyle x^2 + 1}$, som i eksempel 8.

Vi tar ikke med utregningen her, men utfører vi polynomdivisjonen (x³ + 2) : (x² + 1), får vi x, og −x + 2 i rest.

Det vil si at

$f(x) = \frac{\displaystyle x^3 + 2}{\displaystyle x^2 + 1} = x + \frac{\displaystyle −x + 2}{\displaystyle x^2 + 1}$

I den nye brøken har teller lavere grad enn nevner, så brøken vil gå mot 0 når x → ±∞. Vi kan eventuelt verifisere dette ved å dividere alle ledd i teller og nevner med høyeste grad av x, som er 2:

$\frac{\displaystyle −x + 2}{\displaystyle x^2 + 1} = \frac{\displaystyle \frac{−x}{x^2} + \frac{2}{x^2}}{\displaystyle \frac{x^2}{x^2} + \frac{1}{x^2}} = \frac{\displaystyle \frac{−1}{x} + \frac{2}{x^2}}{\displaystyle 1 + \frac{1}{x^2}}$

Delbrøkene går mot 0 når x → ±∞, så vi står igjen med $\frac{\displaystyle 0}{\displaystyle 1} = 0$.

Når brøken forsvinner, blir funksjonsuttrykket $f(x) = x$.

Så y = x er en skråasymptote for f(x).

Med andre funksjonstyper vil det variere hva som skjer når en brøk går mot ${\large \frac{0}{0}}$ eller ${\large \frac{\infty}{\infty}}$. Et godt analyseverktøy er da l′Hôpitals regel, som baserer seg på derivasjon. Denne regelen beskrives i artikkelen om l′Hôpitals regel.

Asymptoter formelt

Ved hjelp av lim-terminologien vi lærer i artikkelen om kontinuitet og grenser kan vi definere asymptoter slik:

y = k er en horisontal asymptote for f(x) hvis $\displaystyle \lim_{x \to +\infty}f(x) = k$ eller $\displaystyle \lim_{x \to −\infty}f(x) = k$
y = ax + b er en skråasymptote for f(x) hvis $\displaystyle \lim_{x \to +\infty}f(x) = ax + b$ eller $\displaystyle \lim_{x \to −\infty}f(x) = ax + b$
x = k er en vertikal asymptote for f(x) hvis $\displaystyle \lim_{x \to k^{\large +}}f(x) = \pm \infty$ eller $\displaystyle \lim_{x \to k^{\large −}}f(x) = \pm \infty$

Dersom vi tillater at a i uttrykket ax + b kan være 0, vil en horisontal asymptote være et spesialtilfelle av en skråasymptote.

Kilder

- Gulliksen, T. & Hole, A. (2010). Matematikk i praksis. Universitetsforlaget

1. juni 20178. mars 2025

Kontinuitet og grenser

For å kunne arbeide med funksjoner på en seriøs måte, må vi forstå begrepene kontinuitet og grenser.

Kontinuitet

At noe er kontinuerlig betyr at det er uavbrutt. Grafen til en kontinuerlig funksjon kan vi altså tegne uten å løfte blyanten.

Eksempel 1:

f(x) = x² + 3x − 2 er en kontinuerlig funksjon. Vi kan tegne grafen uten å løfte blyanten:

En kontinuerlig graf

Det motsatte av kontinuerlig er diskontinuerlig.

Eksempel 2:

En tabell som viser pris som funksjon av vekt på brev inntil 100 gram i Norge (januar 2013) er vist under.

Vekt inntil (g)	20	50	100
Pris (kr)	9,50	15	17

Denne funksjonen er diskontinuerlig, grafen kan ikke tegnes uten å løfte blyanten, den hopper fra 9,5 direkte til 15 og så direkte til 17:

En diskontinuerlig graf

Eksempel 3:

Det er ikke slik at alle funksjoner gitt ved en forskrift er kontinuerlige og alle gitt ved en tabell er diskontinuerlige. Funksjonen $f(x) = \frac{\displaystyle|x|}{\displaystyle x}$ er for eksempel diskontinuerlig. Grafen hopper fra −1 til 1 ved x = 0.

En diskontinuerlig graf

Eksempel 4:

Den rasjonale funksjonen $f(x) = \frac{\displaystyle 1}{\displaystyle x}$ er en diskontinuerlig funksjon. Grafen hopper fra minus uendelig til uendelig ved x = 0.

En diskontinuerlig graf

Dårlige kalkulatorer og dataprogrammer tegner gjerne en strek mellom punktene der grafen forsvinner ut av syne vertikalt, men det er feil. De to kurvehalvdelene er helt atskilt.

Alle polynomfunksjoner er kontinuerlige for alle x. Det samme gjelder rasjonale funksjoner, bortsett fra for x-verdier som gjør nevneren lik 0.

Hvis vi summerer, subtraherer eller multipliserer to kontinuerlige funksjoner, blir resultatet også en kontinuerlig funksjon. Det samme gjelder ved divisjon, bortsett fra i punkter der divisor er 0. Også hvis vi lar en kontinuerlig funksjon være argument til en annen kontinuerlig funksjon blir resultatet også en kontinuerlig funksjon. Dette er et viktig resultat som blir mer interessant når vi har blitt kjent med flere funksjonstyper.

Oppgave 1:

Gitt funksjonene $f(x) = x^2 + 3x − 1$ og $g(x) = x^2 − 4$. Hvilke av følgende kombinasjoner vil være kontinuerlige? For hvilke x-verdier vil vi eventuelt få diskontinuiteter?

$f(x) + g(x)$
$f(x) − g(x)$
$f(x) \cdot g(x)$
$\frac{\displaystyle f(x)}{\displaystyle g(x)}$
$f(g(x))$

Se løsningsforslag

Grenser

Vi starter med å studere grafen til den rasjonale funksjonen $f(x) = \frac{\displaystyle 1}{\displaystyle x^2 + 1}$, vist under, og tar for oss en tilfeldig valgt x-verdi, x = 1, med den tilhørende funksjonsverdien f(1) = 0,5.

Graf for å studere grenseverdier

Vi ser at når x nærmer seg 1, nærmer funksjonsverdien seg 0,5. Jo nærmere x-verdien kommer 1, jo nærmere kommer f(x) 0,5. Det betyr at 0,5 er en grense for f(x) når x nærmer seg 1.

I matematisk terminologi brukes uttrykket lim for grense, det kommer av det latinske limes, noe vi gjenkjenner i det engelske limit. For å vise at x nærmer seg en bestemt verdi, bruker vi en pil.

$\displaystyle \lim_{x \to 1}f(x) = 0,5$

betyr altså at 0,5 er en grense for f(x) når x nærmer seg 1.

Men hva skjer med $f(x) = \frac{\displaystyle 1}{\displaystyle x^2 + 1}$ når x blir større og større? Det kan se ut som om grafen nærmer seg 0, allerede en plass mellom x = 4 og x = 5 faller funksjonsverdien under 0,05:

Graf for å studere grenseverdier

En plass mellom x = 31 og x = 32 faller funksjonsverdien under 0,001:

Graf for å studere grenseverdier

Og faktisk kommer funksjonsverdien nærmere og nærmere 0, jo større x blir. Den blir aldri 0, men vi kan komme så nærme vi vil ved å la x bli stor nok. Det betyr at 0 er en grense for f(x) når x nærmer seg uendelig. Eller i lim-terminologi:

$\displaystyle \lim_{x \to \infty}f(x) = 0$

Oppgave 2:

Bruk terminologien med lim til å uttrykke følgende:

1 er en grense for f(x) når x nærmer seg 0.

0 er en grense for f(x) når x nærmer seg minus uendelig.

Se løsningsforslag

Å finne grenseverdien til en sum av to funksjoner er enkelt. Vi har at hvis

$\displaystyle \lim_{x \to a}f(x) = r$

$\displaystyle \lim_{x \to a}g(x) = s$

vil

$\displaystyle \lim_{x \to a}\big[f(x) + g(x)\big] = r + s$

Vi finner altså grensen til en sum av to funksjoner ved å beregne summen av grensene. Tilsvarende gjelder for subtraksjon, multiplikasjon, divisjon og sammensetning av funksjoner.

Mer om kontinuitet

La oss se på funksjonen $f(x) = \frac{\displaystyle |x|}{\displaystyle x}$ igjen:

En diskontinuerlig graf

Hva er grenseverdien for f(x) når x nærmer seg 0? Vi ser av grafen at hvis x nærmer seg 0 fra høyre, er grenseverdien 1. Men hvis x nærmer seg 0 fra venstre, er grenseverdien −1. Vi sier at den høyresidige grenseverdien er 1 og den venstresidige grenseverdien er −1. I lim-terminologi skriver vi det slik:

$\displaystyle \lim_{x \to 0^{\large +}}f(x) = 1$

$\displaystyle \lim_{x \to 0^{\large −}}f(x) = −1$

Vi bruker altså et plusstegn til å angi høyresidig grenseverdi, og et minustegn til å angi venstresidig grenseverdi. At disse to grensene ikke er like betyr at det ikke eksisterer noen generell grenseverdi for f(x) når x nærmer seg 0. Vi ser også at funksjonen ikke er definert for x = 0. Dette i motsetning til funksjonen $f(x) = \frac{\displaystyle 1}{\displaystyle x^2 + 1}$ vi også så på tidligere:

Kontinuerlig graf

Hvis x nærmer seg 1 fra høyre, er grenseverdien 0,5. Det samme hvis x nærmer seg 1 fra venstre. Den generelle grenseverdien eksisterer altså. Funksjonsverdien når x = 1 er også 0,5. Forskjellen mellom de to funksjonene skyldes at $f(x) = \frac{\displaystyle 1}{\displaystyle x^2 + 1}$ er kontinuerlig når x = 1, mens $f(x) = \frac{\displaystyle |x|}{\displaystyle x}$ ikke er det når x = 0. Og det er nettopp dette vi benytter til å definere kontinuitet.

En funksjon er kontinuerlig i et punkt, a, hvis

Den er definert i a.
Grenseverdien i a eksisterer.
Grenseverdien er den samme som funksjonsverdien i a.

Vi husker at grenseverdien eksisterer hvis den høyresidige og venstresidige grenseverdien er lik. Med andre ord:

f(x) er kontinuerlig i et punkt, a, hvis

$\displaystyle \lim_{x \to a^{\large +}}f(x) = \displaystyle \lim_{x \to a^{\large −}}f(x) = f(a)$

Kontinuitet ved delt funksjonsforskrift

I artikkelen om funksjonsforskrift ser vi at vi ved delt funksjonsforskrift kan ha forskjellige funksjonsforskrifter for forskjellige definisjonsmengder, slik som i eksempel 5 under. I overgangene mellom forskriftene kan det oppstå diskontinuiteter.

Eksempel 5:

Vi skal avgjøre om funksjonen f(x) er kontinuerlig i x = 1, når den er gitt som:

$f(x) =
\begin{cases}
x + 1 & \text{når } x < 1 \\
2 & \text{når } x = 1 \\
2x & \text{når } x > 1
\end{cases}
$

Den venstresidige grenseverdien finner vi å se på funksjonsforskriften når x < 1. Selv om 1 egentlig ikke er med i definisjonsmengden, finner vi grensen ved å sette inn x = 1, og vi får f(x) = 1 + 1 = 2.

Den høyresidige grenseverdien finner vi å se på funksjonsforskriften når x > 1. Selv om 1 egentlig ikke er med i definisjonsmengden, finner vi grensen ved å sette inn x = 1, og vi får f(x) = 2 · 1 = 2.

I selve punktet, x = 1, er det oppgitt at funksjonsverdien er 2.

Siden de tre verdiene er like, er funksjonen kontinuerlig i x = 1. Grafen til funksjonen er vist under. Høyre og venstre del av grafen møtes i (1, 2), der er ingen diskontinuitet.

Graf satt sammen av tre funksjonsforskrifter

Oppgave 3

Funksjonen f(x) er gitt ved delt funksjonsforskrift.

$f(x) =
\begin{cases}
x + 2 & \text{når } x < 2 \\
4 & \text{når } x = 2 \\
2x − 2 & \text{når } x > 2
\end{cases}
$

Avgjør om funksjonen er kontinuerlig i x = 2.

Se løsningsforslag

Oppgave 4:

Avgjør om funksjonen f(x) = |x| er kontinuerlig i x = 0.

Hint: Del funksjonen opp i én funksjonsforskrift for x < 0, én for x = 0 og én for x > 0.

Skjermfilm Se film med løsningsforslag

Mer om grenser

La oss til slutt se på grensebegrepet med formelle øyne.

I artikkelen om intervaller introduserer vi åpne intervaller, ⟨p, q⟩. I et åpent intervall er ikke p og q med i selve intervallet, like fullt angir p og q intervallets yttergrenser. Dette er fordi vi kan komme så nærme disse grensene vi bare vil.

På samme måte kan vi tenke oss grenseverdier for funksjoner:

L er en grense for en funksjon, f(x), når x nærmer seg en verdi, a, hvis vi kan få f(x) så nærme L vi bare vil ved å velge x nærme nok a.

Det krever litt tankearbeid og modning å forstå dette argumentet, prøv å danne deg et mentalt bilde.

En beskrivelse av en grense som den vi ga over vil alltid ha en viss usikkerhet knyttet til språkbruken. Hva mener vi for eksempel med «nærme nok»? For å få en presis definisjon må vi bruke matematisk terminologi. Vi sier det på denne måten:

$\fbox{$\begin{align} &\displaystyle \lim_{x \to a}f(x) = L \\
&\text{betyr at det for alle tall } \epsilon > 0 \\
&\text{finnes et tall } \delta > 0 \\
&\text{slik at når } 0 < |x − a| < \delta \\
&\text{er } |f(x) − L| < \epsilon \end{align}$}$

Dette kalles en epsilon-delta-definisjon fordi den bruker de greske bokstavene epsilon og delta. Epsilon-delta-argumentasjon brukes mye i bestemte typer bevis, så det kan være lurt å forsøke å forstå denne definisjonen. Den er ikke så kryptisk som den kan se ut til.

Skjermfilm Se film som bruker GeoGebra til å illustrere definisjonen av grenseverdi

Last ned GeoGebra-fila som brukes i filmen

Kilder

- Gulliksen, T. & Hole, A. (2010). Matematikk i praksis. Universitetsforlaget

31. mai 201716. januar 2025

Delt funksjonsforskrift

Hva er delt funksjonsforskrift?

Ved delt funksjonsforskrift bruker vi forskjellige funksjonsforskrifter for forskjellige intervaller på tallinja.

Eksempel 1:

Et krydder i løsvekt koster kr 9 per gram ved kjøp inntil 25 gram, kr 8 per gram ved kjøp av 25 gram eller mer, inntil 100 gram, og kr 7 per gram ved kjøp på 100 gram eller mer.

En funksjon som regner ut pris basert på vekt i gram vil være f(x) = 9x når 0 ≤ x < 25, f(x) = 8x når 25 ≤ x < 100 og f(x) = 7x når 100 ≤ x. For å angi disse tre funksjonsforskriftene under ett, bruker vi en delt funksjonsforskrift, som vi angir med en klammeparentes på denne måten:

$ f(x) = \begin{cases} 9x & \quad \text{for } 0\leq x < 25\\ 8x & \quad \text{for } 25\leq x < 100\\ 7x & \quad \text{for } 100\leq x\\ \end{cases}$

Hvis vi så for eksempel skal regne ut prisen på 44 gram krydder, ser vi at 44 er i det midterste intervallet, og vi får f(44) = 8 · 44 = 352. Skal vi regne ut prisen på 12 gram, ser vi at 12 er i det øverste intervallet, og vi får f(12) = 9 · 12 = 108.

Eksempel 2:

Vi kjenner begrepet absoluttverdi som «et tall uten fortegn». Det vil for eksempel si at absoluttverdien til både 3 og −3 er 3. Absoluttverdi angir vi med en vertikal strek på hver side av uttrykket vi vil ta absoluttverdien til, for eksempel |−3|. Vi har altså at |x| = |−x|, for alle tall, x.

Absoluttverdifunksjonen f(x) = |x| skifter fortegn på negative tall, og lar andre tall være som de er. Dette kan vi uttrykke ved hjelp av delt funksjonsforskrift:

$ f(x) = \begin{cases} \;\;x & \quad \text{for } x\geq 0\\ −x & \quad \text{for } x< 0\\ \end{cases}$

Hvis vi så for eksempel skal regne ut f(3), ser vi at 3 er i det øverste intervallet, og vi får f(3) = 3. Skal vi regne ut f(−3), ser vi at −3 er i det nederste intervallet, og vi får f(−3) = −(−3) = 3.

Praktisk bruk av delt funksjonsforskrift

I eksempel 3 og 4 ser vi på en situasjon fra den virkelige verden som vi trenger delt funksjonsforskrift for å modellere.

Eksempel 3:

Vi har en fuglemater med to par hull. Ett par midt på og ett par i bunnen:

Bilde av fuglemater med to par hull

Vi skal så sette opp en funksjon som beskriver hvor mye fuglefôr det til enhver tid er i materen.

Vi antar at det hele tiden er fuger og spiser, så lenge det er fôr. Siden fuglemateren er en sylinder, er det ikke noen variasjoner i formen som påvirker hvor fort fôrnivået synker. Det eneste vi trenger å ta hensyn til er altså hvor fort fuglene spiser, og hvor mange som kan spise av gangen.

Så lengde det er samme antall fugler som spiser, avtar fôrmengden i et konstant forhold til hastigheten de spiser i. Mengden fôr beskrives derfor av en lineær funksjon, på formen f(t) = at + b, der t er tiden i minutter siden materen ble fylt.

Vi observerer at det tar 45 minutter før fuglemateren er halvfull.

At materen er full til å begynne med, og halvfull etter 45 minutter, kan vi matematisk uttrykke som at linjen funksjonen representerer går gjennom punktene (0,100) og (45, 50), der første koordinat representerer tiden i minutter og andre koordinat hvor mange prosent mat som er igjen.

I artikkelen om representasjonsformer lærer vi å finne funksjonsforskriften til en lineær funksjon som går gjennom to gitte punkter, (x₁, y₁) og (x₂, y₂) ved å finne

$a = \frac{\displaystyle y_2 − y_1}{\displaystyle x_2 − x_1}$

$b = y_1− ax_1$

I vårt tilfelle får vi

$a = \frac{\displaystyle 50 − 100}{\displaystyle 45 − 0} = −\frac{\displaystyle 10}{\displaystyle 9}$

$b = 100− (−\frac{\displaystyle 10}{\displaystyle 9} \cdot 0) = 100$

Så funksjonsforskriften blir

$f(t) = −\frac{\displaystyle 10}{\displaystyle 9}t + 100$

Når 45 minutter er gått, vil det ikke være mer fôr å hente i de øverste hullene, så resten av tiden kan bare halvparten så mange fugler spise, og det vil ta dobbelt så lang tid, altså 90 minutter å tømme resten av materen. Totalt går det altså 45 + 90 = 135 minutter fra materen er fylt til den er tom. Dette kan vi modellere ved å si at linjen funksjonen representerer går gjennom punktene for halvfull og tom, (45,50) og (135, 0).

Nå får vi at

$a = \frac{\displaystyle 0 − 50}{\displaystyle 135 − 45} = −\frac{\displaystyle 5}{\displaystyle 9}$

$b = 50 − (−\frac{\displaystyle 5}{\displaystyle 9} \cdot 45) = 75$

Så funksjonsforskriften blir

$f(t) = −\frac{\displaystyle 5}{\displaystyle 9}t + 75$

Så setter vi disse to funksjonsforskriftene sammen i et uttrykk med delt funksjonsforskrift:

$f(t) = \begin{cases}
−\frac{\displaystyle 10}{\displaystyle 9}t + 100 & \; \text{for } 0 \leq t < 45\\
\\
−\frac{\displaystyle 5}{\displaystyle 9}t + 75 & \;\text{for } 45 \leq t \leq 135 \\ \end{cases}$

Her tok vi med tallet 45 i det siste intervallet, men vi kunne gjerne tatt det det med i det første. Modellen er såpass upresis at det egentlig ikke er noe som tilsier det ene eller det andre. Og begge deler gir samme svar, siden funksjonen er kontinuerlig når t = 45. (En diskontinuerlig funksjon ville jo vært underlig, da måtte fôrnivået plutselig ha endret seg magisk etter 45 minutter.)

En graf som viser hvor mange prosent fôr som er igjen i materen som funksjon av tiden er vist under:

Graf som viser hvor mye fôr som er igjen i en fuglemater som funksjon av tiden

Oppgave 1:

Bildet under viser en fuglemater med 3 par hull, ett par i bunnen, ett par en tredjedel opp, og ett par to tredjedeler opp.

Bilde av fuglemater med tre par hull

Fra materen er full til den er to tredels full går det 20 minutter. Finn fram til en delt funksjonsforskrift som angir mengden fôr (fra 100 % til 0 %) som er
tilbake i fuglemateren basert på antall minutter siden den ble fylt helt opp.

Du kan gjøre samme forutsetninger som i eksempel 3, at det hele tiden er fuger og spiser så lenge det er fôr, og at det ikke noen variasjoner i formen som påvirker hvor fort fôrnivået synker.

Se løsningsforslag

Kilder

- Thomas, G.B., Finney R.L. (1988). Calculus and Analytic Geometry. Addison-Wesley.
- matematikk.org