Forfatter: Sjefen

Dersom vi er ute etter å finne gjennomsnittsvekta på fisk i et oppdrettsanlegg, kan vi ta opp all fisken, veie hvert individ, og ut fra det beregne det eksakte gjennomsnittet.

I praksis vil imidlertid en slik fremgangsmåte være lite hensiktsmessig. I stedet gjør vi et tilfeldig utvalg, og gir på bakgrunn av dette et estimat, det vil si et anslag, av gjennomsnittsvekta.

Vi kan nøye oss med å ta opp én enkelt fisk, men intuitivt skjønner vi at det vil være bedre å ta opp flere og basere anslaget på gjennomsnittsvekta.

I artikkelen om sentralgrenseteoremet ser vi at hvis vi har n variabler som er uavhengige og har samme fordeling, med forventning μ og varians σ², vil gjennomsnittet av variablene være tilnærmet normalfordelt med forventning μ og varians $\frac{\displaystyle \sigma^2}{\displaystyle n}$. Vi antyder at n bør være > 30 for at tilnærmingen skal være god, men hvis vi kan anta at variablene i utgangspunktet er tilnærmet normalfordelt, kan vi fire på dette kravet.

Sørger vi for at fisken vi tar opp blir valgt tilfeldig, vil altså variansen til gjennomsnittsvekta være $\frac{\displaystyle \sigma^2}{\displaystyle n}$, der n er antall fisk vi har veid og σ² variansen til vekta i fiskepopulasjonen. Jo flere fisk vi veier, jo større blir nevneren i brøken, og jo mindre blir variansen til gjennomsnittet.

For å angi et estimat bruker vi en estimator. For å indikere at en variabel er en estimator, bruker vi en «hatt», for eksempel er $\hat \theta$ en estimator for $\theta$.

Dersom en estimator gir den forventede verdien, det vil si at $E(\hat \theta) = \theta$, kalles estimatoren forventningsrett. I motsatt fall er den forventningsskjev.

Estimere forventning og standardavvik

Ofte er vi ute etter å estimere en forventningsverdi, μ, hos en populasjon basert på målinger i et tilfeldig utvalg. Som estimator, $\hat \mu$, bruker vi da gjennomsnittet av målingene. Har vi for eksempel gjort n målinger med resultater X₁, X₂, X₃ … X_n, blir estimatoren

$\fbox{$\hat \mu = \overline X = \frac{\displaystyle X_1 + X_2 + \dots + X_n}{\displaystyle n}$}$
 
Eksempel 1:

Vi har tatt opp og veid 13 laks fra et oppdrettsanlegg. Laksene veide
3,9, 3,6, 5,1, 4,8, 3,7, 3,2, 4,6, 5,4, 3,0, 4,2, 3,8, 4,4 og 4,1 kg.

Et forventningsrett estimat for gjennomsnittsvekta til all laksen i anlegget er da gjennomsnittet av veiingene:

$\hat \mu = \overline X = {\large \frac{3{,}9 + 3{,}6 + 5{,}1 + 4{,}8 + 3{,}7 + 3{,}2 + 4{,}6 + 5{,}4 + 3{,}0 + 4{,}2 + 3{,}8 + 4{,}4 + 4{,}1}{13}} \approx 4{,}14$. Altså om lag 4,14 kg.

Det er imidlertid sjelden vi beregner gjennomsnitt for hånd. I stedet bruker vi statistikkfunksjoner på en kalkulator, eller funksjonen gjennomsnitt i Excel eller GeoGebra.

Oppgave 1:

En enhet i en bedrift produserer støtfangere. Dagsproduksjonen på seks tilfeldig valgte dager er
210, 220, 210, 225, 220 og 217 enheter. Finn et forventningsrett estimat for hvor mange støtfangere som produseres daglig.

Se løsningsforslag

Rapportering

Hvor sikkert et estimat er, sier ikke $\hat \mu$ noe om, men estimater har gjerne en usikkerhet knyttet til seg. Rimelig nok er denne usikkerheten avhengig av antall målinger estimatet er basert på. Jo færre målinger, jo større usikkerhet. Usikkerheten er også avhengig av standardavviket, σ, til populasjonen vi estimerer i. Jo større σ er, jo større er spredningen, og jo mer usikkert er estimatet. Dersom σ er 0, har vi ikke spredning, og en enkelt måling vil gi et estimat uten usikkerhet.

Når vi angir et estimat, er det vanlig å angi usikkerheten til estimatet, på formen «estimert verdi pluss/minus standardavviket til estimatoren».

Dersom estimatoren er gjennomsnittet av n målinger, er altså variansen til estimatoren $\frac{\displaystyle \sigma^2}{\displaystyle n}$, og følgelig standardavviket til estimatoren $\frac{\displaystyle \sigma}{\displaystyle \sqrt n}$. Så vi har

$\fbox{Rapportering: $\hat \mu \pm \frac{\displaystyle \sigma}{\displaystyle \sqrt n}$}$
 
Eksempel 2:

I eksempel 1 fant vi at gjennomsnittsvekta på 13 laks vi tok opp var om lag 4,14 kg.

Hvis standardavviket til vekta i fiskepopulasjonen er σ = 0,7, kan vi angi estimatet til gjennomsnittsvekta slik:

$4{,}14 \pm \frac{\displaystyle 0{,}7}{\displaystyle \sqrt{13}} \approx 4{,}14 \pm 0{,}19$

Oppgave 2:

I oppgave 1 estimerte vi dagsproduksjonen av støtfangere basert på at produksjonen på seks forskjellige dager var henholdsvis 210, 220, 210, 225, 220 og 217 enheter. Anta at standardavviket til produksjonen er σ = 5,8, og angi estimert dagsproduksjon i form av en rapportering.

Se løsningsforslag

Rapportering ved ukjent standardavvik

Av og til kjenner vi en populasjons standardavvik, for eksempel hvis avviket skyldes dokumenterte unøyaktigheter i et måleinstrument. Men som regel er standardavviket ukjent, og må estimeres, det også.

Det vil da være naturlig å ta utgangspunkt i det standardavviket vi kan beregne ut fra de målingene vi har gjort, utvalgsstandardavviket. I artikkelen om måltall i statistikk ser vi at hvis vi har gjort n målinger av X og beregnet at gjennomsnittet er X, er utvalgsstandardavviket gitt ved

$S = \sqrt \frac{\displaystyle \sum_{i = 1}^n(X_i – \overline X)^2}{\displaystyle n – 1}$

Imidlertid er det sjelden vi beregner standardavvik for hånd. I stedet bruker vi statistikkfunksjoner på en kalkulator, eller funksjonen stdav.s i Excel eller funksjonen stdav i GeoGebra.

Utvalgsvariansen, S² vil være et forventningsrett estimat for variansen i en fordeling, σ². På grunn av at kvadratrotfunksjonen ikke er lineær, vil imidlertid ikke utvalgsstandardavviket, S, som estimat for standardavviket, σ, være forventningsrett. Feilen er imidlertid så liten at det er vanlig å bruke utvalgsstandardavviket som estimator for en fordelings standardavvik:

$\hat \sigma = S$

Formelen for rapportering blir da

$\fbox{Rapportering: $\hat \mu \pm \frac{\displaystyle S}{\displaystyle \sqrt n}$}$

Eksempel 3:

I eksempel 1 fant vi at gjennomsnittsvekta på 13 laks fra et oppdrettsanlegg var
3,9, 3,6, 5,1, 4,8, 3,7, 3,2, 4,6, 5,4, 3,0, 4,2, 3,8, 4,4 og 4,1 kg.

Et estimat for standardavviket til vekta er da

$\hat \sigma = S \approx 0{,}711$, beregnet ved hjelp av stdav.s i Excel.

En rapportering av gjennomsnittsvekta blir derfor

$4{,}14 \pm \frac{\displaystyle 0{,}711}{\displaystyle \sqrt{13}} \approx 4{,}14 \pm 0{,}20$

Oppgave 3:

I oppgave 1 så vi at dagsproduksjonen av støtfangere på seks tilfeldig valgte dager i en bedrift var 210, 220, 210, 225, 220 og 217 enheter.

Estimer standardavviket til produksjonen, og presenter estimert gjennomsnitt i form av en rapportering.

Se løsningsforslag

Konfidensintervaller

Å estimere en forventningsverdi kaller vi å angi et punktestimat, fordi vi anslår et punkt på tallinja. Vi skal nå se på konfidensintervaller, der vi angir et intervall på tallinja som med en viss sannsynlighet inneholder den riktige forventningsverdien. For eksempel at gjennomsnittsvekta på laks i eksempel 1 med 95 % sannsynlighet ligger mellom 3,8 og 4,5 kg.

For å finne ut hvordan vi estimerer grensene i et konfidensintervall, starter vi med å se på en standard normalfordeling, altså en normalfordeling med forventning μ = 0 og standardavvik σ = 1.

Figuren under viser en standard normalfordelingskurve der 95 % av arealet under kurven er markert. Det vil si at hvis vi gjentatte ganger velger en tilfeldig variabel fra denne fordelingen, vil den 95 % av gangene havne innenfor det fargede området, altså mellom −z og z. Arealet er gitt ved G(z) − G(−z) = 0,95. Det vil si at G(z) − (1 − G(z)) = 0,95 ⇒ 2G(z) = 0,95 + 1 ⇒ G(z) = 0,975.

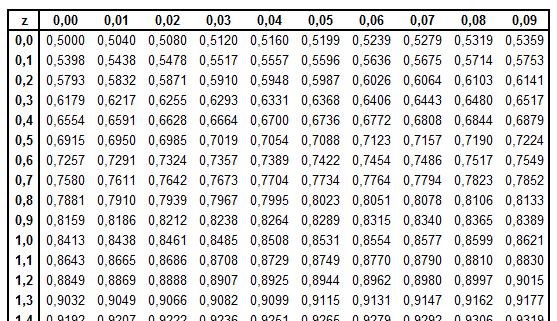
Når vi tidligere har brukt normalfordelingstabellen, har vi kjent z og brukt tabellen til å finne G(z). Nå skal vi gå andre veien. Vi kjenner G(z) og skal finne z. Vi leter i tabellen og finner 0,9750 i rad 1,9 og kolonne 0,06:

Det vil si at z = 1,96 og følgelig −z = −1,96. Vi ser at det stemmer bra med figuren over.

I figuren under er 99 % av arealet markert. Arealet her er gitt ved G(z) − G(−z) = 0,99. Det vil si at G(z) − (1 − G(z)) = 0,99 ⇒ 2G(z) = 0,99 + 1 ⇒ G(z) = 0,995.

I normalfordelingstabellen finner vi ikke nøyaktig 0,995, men G(2,57) = 0,9949 og G(2,58) = 0,9951. Vi tar gjennomsnittet og setter z = 2,575 og −z = −2,575. Vi ser at det stemmer bra med figuren over.

Det betyr at for en standard normalfordelt variabel er [−1,96, 1,96] et 95 % konfidensintervall, og [−2,58, 2,58] er et 99 % konfidensintervall.

I artikkelen om normalfordelingen ser vi at hvis vi har en variabel, X, som er normalfordelt N(μ, σ²), standardiserer vi variabelen ved å beregne $Z = \frac{\displaystyle X – \mu}{\displaystyle \sigma}$, som er normalfordelt N(0, 1).

Nå skal vi gå motsatt vei. Løser vi likningen $Z = \frac{\displaystyle X – \mu}{\displaystyle \sigma}$ med hensyn på X, får vi X = Z · σ + μ. Det betyr at hvis Z er standard normalfordelt, N(0, 1), blir X = Z · σ + μ normalfordelt med forventning μ og standardavvik σ, N(μ, σ²).

Vi så at i en standard normalfordeling var grensene for et 95 % konfidensintervall om lag ± 1,96. Et 95 % konfidensintervall for en fordeling som er N(μ, σ²) blir derfor

[μ − 1,96 · σ, μ + 1,96 · σ]

Eller mer kompakt uttrykt som μ ± 1,96 · σ.

Vi ser at intervallet er sentrert rundt forventningen, μ, og blir bredere jo større σ blir. Det er rimelig. Jo større standardavvik, jo mer usikkert er estimatet, og jo bredere må intervallet være for at vi skal være 95 % sikre på at det rommer gjennomsnittet.

Da vi estimerte gjennomsnitt i en populasjon, så vi at standardavviket til estimatet var $\frac{\displaystyle \sigma}{\displaystyle \sqrt n}$.

Hvis gjennomsnittet av n målinger i en fordeling med standardavvik σ er X, blir derfor et 95 % konfidensintervall for gjennomsnittet

$[\overline X \, – 1{,}96 \cdot \frac{\displaystyle \sigma}{\displaystyle \sqrt n}, \, \overline X + 1{,}96 \cdot \frac{\displaystyle \sigma}{\displaystyle \sqrt n}]$

Eller på kompakt form

$\overline X \pm 1{,}96 \cdot \frac{\displaystyle \sigma}{\displaystyle \sqrt n}$

Vi ser at bredden på et konfidensintervall ikke bare avhenger av σ, men også av antall målinger. Jo flere målinger, jo smalere blir konfidensintervallet.

Vi så i figuren over at i et 95 % og et 99 % konfidensintervall er grensen for z henholdsvis om lag 1,96 og 2,58. Tilsvarende kan vi finne at grensen er om lag 1,65 for et 90 % konfidensintervall.

I kortform:

$\fbox{$\begin{align}\, \\
&\text{Konfidensintervaller:}\\
&\text{90 %: } \overline X \pm 1{,}65 \cdot \frac{\displaystyle \sigma}{\displaystyle \sqrt n} \\
&\text{95 %: } \overline X \pm 1{,}96 \cdot \frac{\displaystyle \sigma}{\displaystyle \sqrt n} \\
&\text{99 %: } \overline X \pm 2{,}58 \cdot \frac{\displaystyle \sigma}{\displaystyle \sqrt n} \\
\end{align}$}$

Vi ser at intervallene blir bredere jo høyere konfidens vi ønsker.

Eksempel 4:

I eksempel 1 fant vi at gjennomsnittsvekta på 13 laks vi tok opp var om lag 4,14 kg.

Hvis vi vet at populasjonen er normalfordelt med standardavvik σ = 0,7, vil vi få følgende 90 %, 95 % og 99 % konfidensintervaller for laksens gjennomsnittsvekt:

90 %: $4{,}14 \pm 1{,}65 \cdot \frac{\displaystyle 0{,}7}{\displaystyle \sqrt{13}} \approx 4{,}14 \pm 0{,}32 = [3{,}82, 4{,}46]$

95 %: $4{,}14 \pm 1{,}96 \cdot \frac{\displaystyle 0{,}7}{\displaystyle \sqrt{13}} \approx 4{,}14 \pm 0{,}38 = [3{,}76, 4{,}52]$

99 %: $4{,}14 \pm 2{,}58 \cdot \frac{\displaystyle 0{,}7}{\displaystyle \sqrt{13}} \approx 4{,}14 \pm 0{,}50 = [3{,}64, 4{,}64]$

Oppgave 4:

I oppgave 1 estimerte vi dagsproduksjonen av støtfangere basert på at produksjonen i seks forskjellige dager var henholdsvis 210, 220, 210, 225, 220 og 217 enheter. Anta at produksjonen er normalfordelt med standardavvik σ = 5,8, og angi 95 % og 99 % konfidensintervaller for gjennomsnittsproduksjonen.

Se løsningsforslag

Vi har nå sett på 90 %, 95 % og 99 % konfidensintervaller, men andre prosenter er selvsagt også mulig. Det generelle uttrykket er

$\fbox{$\begin{align} &\text{Konfidensintervall:} \\
&\overline X \pm {\large z_{\Large \frac{\alpha^\phantom 1}{2}}} \cdot \frac{\displaystyle \sigma}{\displaystyle \sqrt n} \end{align}$}$

Her representerer α den prosentdelen som ligger utenfor konfidensintervallet. Halvparten av α ligger til venstre for, og halvparten av α til høyre for intervallet, som vist under:

$\pm {\large z_{\Large \frac{\alpha^\phantom 1}{2}}}$ er da z-verdiene i yttergrensene av det fargede området.

I et k % konfidensintervall er altså ${\large \frac{\alpha}{2}} = {\large \frac{1 – k}{2}}$, for eksempel ${\large \frac{1 – 0{,}95}{2}} = 0{,}025$ i et 95 % konfidensintervall og ${\large \frac{1 – 0{,}99}{2}} = 0{,}005$ i et 99 % konfidensintervall.

Da vi skulle finne intervallet [−z, z] som utgjorde et 95 % og 99 % konfidensintervall i en standard normalfordeling, gjorde vi et baklengs oppslag i normalfordelingstabellen for å finne z. Dette er tungvint, og det er derfor laget ferdige, omvendte tabeller. I en slik tabell slår vi opp a, og får ut z, slik at arealet under kurven til høyre for z er a.

Dette kalles kvantiltabeller eller fraktiltabeller for normalfordelingen, en kvantiltabell for normalfordelingen finnes på dette nettstedet.

Eksempel 5:

Vi er interessert i å finne et 98 % konfidensintervall for gjennomsnittsvekta til laksen fra eksempel 1.

Vi får at ${\large \frac{\alpha}{2}} = {\large \frac{1 – 0{,98}}{2}} = 0{,}01$. Vi slår opp 0,010 i (kvantil)normalfordelingstabellen og får 2,3263.

Vi har altså at ${\large z_{\Large \frac{\alpha^\phantom 1}{2}}} = {\large z}_{0{,}01}^\phantom 1 \approx 2{,}3263$.

I eksempel 1 fant vi at gjennomsnittsvekta til n = 13 laks var 4,14 kg. Hvis laksepopulasjonen er normalfordelt med standardavvik σ = 0,7, blir altså et 98 % konfidensintervall

$4{,}14 \pm 2{,}3263 \cdot \frac{\displaystyle 0{,}7}{\displaystyle \sqrt{13}} \approx 4{,}14 \pm 0{,}45 = [3{,}69, 4{,}59]$

Oppgave 5:

Bruk metoden fra eksempel 5 til å finne et 97 % konfidensintervall for laksens gjennomsnittsvekt.

Se løsningsforslag

Konfidensintervaller i Excel og GeoGebra

I Excel og GeoGebra finnes egne funksjoner for baklengs oppslag i normalfordelinger, norm.inv i Excel og inversnormalfordeling i GeoGebra. Med disse er det imidlertid $1 – {\large \frac{\alpha}{2}}$ vi slår opp, vi angir altså arealet under normalfordelingskurven til venstre for, ikke til høyre for, ${\large \frac{\alpha}{2}}$.

Funksjonene er inverser av funksjonene norm.fordeling og fordelingnormal, som vi presenterer i artikkelen om normalfordelingen. Der oppgir vi en grenseverdi, og får ut sannsynligheten for at en normalfordelt, tilfeldig variabel er mindre eller lik denne grenseverdien. I de inverse funksjonene oppgir vi sannsynligheten, og får ut grenseverdien. I tillegg må vi også gi inn normalfordelingens forventningsverdi og standardavvik. Excel har også en funksjon, norm.s.inv, som er inversen til norm.s.fordeling. Her trenger vi ikke oppgi forventningsverdi eller standardavvik, verdiene 0 og 1 brukes automatisk. Noe tilsvarende finnes ikke i GeoGebra.

Disse funksjonene er imidlertid ikke veldig interessante når vi skal beregne bredden på konfidensintervaller. Har vi en datamaskin tilgjengelig, kan vi bruke Excel eller GeoGebra til å beregne denne bredden direkte.

I Excel bruker vi funksjonen konfidens.norm, der vi gir inn α samt fordelingens varians og antall elementer i utvalget. (Vi gir altså inn α, ikke ${\large \frac{\alpha}{2}}$.) Excel beregner da avstanden fra utvalgets gjennomsnitt til intervallgrensene. I GeoGebra bruker vi sannsynlighetskalkulatoren, slik det er beskrevet i artikkelen om statistikk med GeoGebra.

Eksempel 6:

Med basis i data fra lakseveiningen i eksempel 1, skal vi bruke Excel til å beregne grensene i et 95 % og et 99 % konfidensintervall for laksens gjennomsnittsvekt. Vi har altså veid 13 fisk og funnet et gjennomsnitt på 4,14 kg. Populasjonen er normalfordelt med standardavvik 0,7.

Skriver vi =konfidens.norm(1-0,95; 0,7; 13) i Excel, får vi ut 0,38. Et 95 prosent konfidensintervall blir derfor om lag

[4,14 − 0,38, 4,14 + 0,38] = [3,76, 4,52].

Skriver vi =konfidens.norm(1-0,99; 0,7; 13) i Excel, får vi ut 0,50. Et 99 prosent konfidensintervall blir derfor om lag

[4,14 − 0,50, 4,14 + 0,50] = [3,64, 4,64].
 

Last ned regneark som beregner 90 – 99 % (normal)konfidensintervaller

 
Oppgave 6:

Bruk Excel til å beregne et 98 % konfidensintervall for gjennomsnittsproduksjonen av støtfangere fra oppgave 1. Vi har altså dagsproduksjoner på henholdsvis 210, 220, 210, 225, 220 og 217 enheter, og vet at produksjonen er normalfordelt med standardavvik 5,8.

Se løsningsforslag

Konfidensintervaller ved ukjent standardavvik

Når vi har brukt normalfordelingen til å lage konfidensintervaller i en populasjon, har vi forutsatt at standardavviket til populasjonen, σ, er kjent. Av og til kjenner vi en populasjons standardavvik, for eksempel hvis avviket skyldes dokumenterte unøyaktigheter i et måleinstrument. Men som regel er standardavviket ukjent, og må estimeres, det også.

Det vil da være naturlig å ta utgangspunkt i det standardavviket vi kan beregne ut fra de målingene vi har gjort, nemlig utvalgsstandardavviket, S, og estimere σ som

$\hat \sigma = S$

I artikkelen om måltall i statistikk ser vi at hvis vi har gjort n målinger av en variabel X og beregnet at gjennomsnittet er X, er utvalgsstandardavviket, S, gitt ved

$S = \sqrt \frac{\displaystyle \sum_{i = 1}^n(X_i – \overline X)^2}{\displaystyle n – 1}$

Bruk av utvalgsstandardavviket innebærer imidlertid at vi innfører en usikkerhet, noe som medfører at normalfordelingen gir et for smalt intervall. I stedet for normalfordelingen bruker vi da en t-fordeling, også kalt Students t-fordeling. t-fordelingen er ikke én enkelt kurve, men en familie med kurver som blir lavere og bredere jo høyere usikkerhet vi har. Denne usikkerheten måler vi i frihetsgrader, v, der økende antall frihetsgrader gir synkende usikkerhet.

Figuren under viser et plott av tre t-kurver med frihetsgrader på henholdsvis v = 1, v = 5 og v = 30, tegnet med henholdsvis grønn, blå og rød linje. Figuren viser også en normalfordelingskurve, tegnet med svart, prikkete linje. Vi ser at t-kurven nærmer seg normalkurven når antall frihetsgrader øker. Ved 30 frihetsgrader er kurvene så å si overlappende.

Når vi skal bruke t-fordelingen ut fra et utvalgsstandardavvik basert på n målinger, setter vi antall frihetsgrader, v, lik antall målinger minus 1, v = n − 1.

t-kurven blir altså bredere jo færre målinger vi har.

Vi har tidligere sett hvordan vi brukte en kvantiltabell for normalfordelingen til å slå opp a og få ut z, slik at arealet under kurven til høyre for z var a. En kvantiltabell for t-fordelingen er tilsvarende, men vi må i tillegg til a også angi antall frihetsgrader, v. På dette nettstedet finnes en kvantiltabell for t-fordelingen. Tabellen går opp til 30 frihetsgrader. Har vi flere frihetsgrader, er t-fordelingen så nærme normalfordelingen at vi i stedet kan bruke kvantiltabellen for normalfordelingen.

Eksempel 7:

I eksempel 3 målte vi vekta på 13 laks, og fant at gjennomsnittet var X ≈ 4,14 kg og utvalgsstandardavviket S ≈ 0,71 kg.

Skulle vi brukt normalfordelingen til å lage et 95 % konfidensintervall for vekta, ville vi basert oss på z_0,025 ≈ 1,96, og fått:

$4{,}14 \pm 1{,}96 \cdot {\large \frac{0{,}71}{\sqrt{13}}} \approx [3{,}75, 4{,}53]$.

Men siden vi baserer oss på utvalgsstandardavviket, bruker vi i stedet (kvantil)t-fordelingstabellen med a = 0,025 og v = 13 − 1 = 12. Vi finner at t_{0,025 (12)} ≈ 2,179 og får:

$4{,}14 \pm 2{,}179 \cdot {\large \frac{0{,}71}{\sqrt{13}}} \approx [3{,}71, 4{,}57]$.

Konfidensintervallet blir litt bredere enn da vi brukte normalfordelingen, dette gjenspeiler usikkerheten ved at bruk av utvalgsstandardavviket basert på så lite som 13 målinger.

Oppgave 7:

I oppgave 1 og 2 fant vi, basert på 6 tilfeldige observasjoner, at gjennomsnittlig antall produserte støtfangere var X= 217 stk., og at produksjonens utvalgsstandardavvik var S = 6 stk. Lag og sammenlikn et 95 % konfidensintervall basert på normalfordeling, med et basert på t-fordeling.

Se løsningsforslag

Når standardavviket til en populasjon er ukjent, beregner vi altså et konfidensintervall som

$\fbox{$\begin{align} &\text{Konfidensintervall:} \\
&\overline X \pm {\large t_{\Large \frac{\alpha^\phantom 1}{2} \,(v)}} \cdot \frac{\displaystyle S}{\displaystyle \sqrt n} \end{align}$}$

For 90 %, 95 % og 99 % konfidensintervaller blir dette

$\fbox{$\begin{align}\, \\
&\text{Konfidensintervaller:}\\
&\text{90 %: } \overline X \pm {\large t_{90 \, \% \,(v)}} \cdot \frac{\displaystyle S}{\displaystyle \sqrt n} \\
&\text{95 %: } \overline X \pm {\large t_{95 \, \% \,(v)}} \cdot \frac{\displaystyle S}{\displaystyle \sqrt n} \\
&\text{99 %: } \overline X \pm {\large t_{99 \, \% \,(v)}} \cdot \frac{\displaystyle S}{\displaystyle \sqrt n} \\
\end{align}$}$

t-fordeling i Excel og GeoGebra

Excel og GeoGebra har mange funksjoner for oppslag i t-fordeling, tilsvarende de som finnes for oppslag i normalfordeling.

I artikkelen om normalfordelingen presenterer vi Excel-funksjonen norm.fordeling og GeoGebra-funksjonen fordelingnormal, som beregner P(X ≤ x) i en vilkårlig normalfordeling. Motsvarende i t-fordelingen heter henholdsvis t.fordeling og fordelingt. I t-fordelingen antas forventningen å være 0 og standardavviket 1, så det trenger vi ikke oppgi. I stedet må vi oppgi antall frihetsgrader. I norm.fordeling er parameterne x, antall frihetsgrader, og sann/usann for kumulativ/ikke-kumulativ sannsynlighet. I fordelingt oppgir vi først antall frihetsgrader, deretter x og true/false for kumulativ/ikke-kumulativ. true/false kan sløyfes, da benyttes kumulativ sannsynlighet, som er det vanligste.

I denne artikkelen presenterte vi inversene til funksjonene nevnt over, norm.inv i Excel og inversnormalfordeling i GeoGebra. Motsvarende for t-fordelingen heter t.inv og inverstfordeling. I Excel er første parameter sannsynligheten og andre antall frihetsgrader, omvendt i GeoGebra.

I denne artikkelen har vi også sett hvordan vi kunne bruke funksjonen konfidens.norm i Excel og sannsynlighetskalkulatoren i GeoGebra til å beregne grensene i et konfidensintervall.

I Excel bruker vi funksjonen konfidens.t til å beregne bredden av et konfidensintervall basert på en t-fordeling. Vi gir da inn α, standardavvik og utvalgsstørrelse. I GeoGebra bruker vi sannsynlighetskalkulatoren, slik det er beskrevet i artikkelen om statistikk med GeoGebra.

Eksempel 8:

I eksempel 7 fant vi at et 95 % konfidensintervall for gjennomsnittsvekta til 13 laks med gjennomsnittsvekt 4,14 og utvalgsstandardavvik 0,711 var

$4{,}14 \pm 2{,}179 \cdot {\large \frac{0{,}71}{\sqrt{13}}} \approx [3{,}71, 4{,}57]$

For å beregne det samme i Excel, skriver vi =konfidens.t(1-0,95; 0,71; 13) og får ut 0,43. Et 95 prosent konfidensintervall blir derfor om lag

[4,14 − 0,43, 4,14 + 0,43] = [3,71, 4,57].
 

Last ned regneark som beregner 90 – 99 % (t)konfidensintervaller

 
Oppgave 8:

I oppgave 7 beregnet vi, basert på 6 tilfeldige observasjoner med gjennomsnitt 217 og utvalgsstandardavvik 6 et 95 % konfidensintervall basert på t-fordeling. Gjør den samme beregningen i Excel.

Se løsningsforslag

Når vi i eksempler og oppgaver har forutsatt at populasjonene er normalfordelte, er det fordi vi har gjort beregninger basert på ganske få målinger. Hvis vi øker antall målinger til 30 eller mer, kan vi imidlertid fire på dette kravet. Sentralgrenseteoremet garanterer at gjennomsnittene i alle tilfeller vil være tilnærmet normalfordelte.

Estimere sannsynligheter

I tidligere avsnitt har vi estimert forventningsverdi og standardavvik. Nå skal vi se hvordan vi kan estimere sannsynligheten for at elementer i en populasjon har en gitt egenskap. Vi antar at hvert element enten har eller ikke har egenskapen, og at det er uavhengighet mellom elementene, slik at vi har en binomisk modell. Vi bruker symbolet $\hat p$ til å estimere sannsynligheten p. Trekker vi n elementer fra populasjonen, og X av disse har den gitte egenskapen, er en forventningsrett estimator
$\hat p = {\large \frac{X}{n}}$.

Standardavviket til estimatoren baseres ikke på et utvalgsstandardavvik, men på at variansen i en binomisk fordeling er Var(X) = np(1 − p), slik vi beskriver i artikkelen om forventning og varians.

Ved å bruke regnereglene fra denne artikkelen, kan vi finne variansen til estimatoren:

$Var(\hat p) = Var(\frac{\displaystyle X}{\displaystyle n}) = {(\frac{\displaystyle 1}{\displaystyle n})}^2Var(X) = {(\frac{\displaystyle 1}{\displaystyle n})}^2(np(1 – p)) = \frac{\displaystyle p(1 – p)}{\displaystyle n}$.

Og standardavviket til estimatoren blir $\sqrt \frac{\displaystyle p(1 – p)}{\displaystyle n}$

Vi ser at standardavviket blir 0 når p = 1 eller p = 0, rimelig nok, siden vi da ikke har spredning i det hele tatt. Størst standardavvik får vi når p = 0,5.

Nå er jo ikke p kjent, dette er jo den ukjente variabelen vi skal estimere, så vi tilnærmer p med den estimerte sannsynligheten, $\hat p$.

Formelen for rapportering i denne modellen blir da

$\fbox{Rapportering: $\overline X \pm \sqrt \frac{\displaystyle \hat p(1 – \hat p)}{\displaystyle n}$}$

Og et konfidensintervall angis som

$\fbox{$\begin{align}&\text{Konfidensintervall:} \\
&\hat p \pm {\large z_{\Large \frac{\alpha^\phantom 1}{2}}} \cdot \sqrt{ \frac{\displaystyle \hat p(1 – \hat p)}{\displaystyle n}} \end{align}$}$

For 90 %, 95 % og 99 % konfidensintervaller blir dette

$\fbox{$\begin{align}\, \\
&\text{Konfidensintervaller:}\\
&\text{90 %: } \hat p \pm 1{,}65 \cdot \sqrt{ \frac{\displaystyle \hat p(1 – \hat p)}{\displaystyle n}} \\
&\text{95 %: } \overline X \pm 1{,}96 \cdot \sqrt{ \frac{\displaystyle \hat p(1 – \hat p)}{\displaystyle n}} \\
&\text{99 %: } \overline X \pm 2{,}58 \cdot \sqrt{ \frac{\displaystyle \hat p(1 – \hat p)}{\displaystyle n}} \\
\end{align}$}$

Da vi estimerte forventning, så vi at vi kompenserte for usikkerheten ved at variansen var ukjent, ved å bruke t-fordeling i stedet for normalfordeling. Det gjør vi ikke når vi estimerer sannsynligheter, vi forutsetter i stedet at vi har n ≥ 30, slik at normalfordelingen gir en god nok tilnærming.

Eksempel 9:

Når vi kaster en vanlig mynt 50 ganger, er forventningsverdien til antall kron 50 · 0,5 = 25. Store avvik fra dette kan tyde på at det er noe juks med mynten.

Vi kaster en mynt vi mistenker er jukset med 50 ganger, og får 33 kron.

Vi estimerer da sannsynligheten for kron med $\hat p = {\large \frac{X}{n}} = {\large \frac{33}{50}}= 0{,}66$.

Vi estimerer standardavviket til estimatoren med $\sqrt{\large \frac{\hat p(1- \hat p)}{n}} = \sqrt{\large \frac{0{,}66(1 – 0{,}66)}{50}} \approx 0{,}067$.

En rapportering av denne sannsynligheten blir da

0,66 ± 0,067

Så ønsker vi å finne 95 % og 99 % konfidensintervaller for den estimerte sannsynligheten.

Fra tidligere eksempler vet vi at vi i et 95 % konfidensintervall har

${\large z_{\Large \frac{\alpha^\phantom 1}{2}}} \approx 1{,}96$

og i et 99 % konfidensintervall har

${\large z_{\Large \frac{\alpha^\phantom 1}{2}}} \approx 2{,}58$

Så et 95 % konfidensintervall blir 0,66 ± 1,96 · 0,067 ≈ [0,53, 0,79].

Og et 99 % konfidensintervall blir 0,66 ± 2,58 · 0,067 ≈ [0,49, 0,83].

Vi ser at et 95 % konfidensintervall ikke fanger opp sannsynligheten for en normal mynt, som er 0,5, men 99 % intervallet gjør det så vidt. Det betyr at estimatet med 95 % sikkerhet indikerer at mynten er jukset med, men ikke med 99 % sikkerhet.

Oppgave 9:

En bedrift som produserer mobilladere, tester 2000 tilfeldige ladere, og finner ut at 35 av dem er defekte.

Finn et estimat for hvor stor sannsynligheten er for at en vilkårlig lader er defekt, og angi resultatet som en rapportering.

Finn deretter et 95 % konfidensintervall for estimatet.

Se løsningsforslag

Å beregne konfidensintervaller for sannsynligheter i Excel er tungvint, men sannsynlighetskalkulatoren i GeoGebra gjør dette enkelt , slik det er beskrevet i artikkelen om statistikk med GeoGebra.

Kilder

• • Ubøe, J. (2011). Statistikk for økonomifag. Gyldendal akademisk
  • Hagen, Per C. (2000). Innføring i sannsynlighetsregning og statistikk. Cappelen akademisk
  • Bhattacharyya, G, Johnson, R.A. (1977) Statistical concepts and methods. John Wiley & Sons