Denne artikkelen gir en oversikt over sentrale begreper og formler for plangeometriske figurer.
Plangeometriske figurer har utstrekning i inntil to retninger, de er flate. Vanlige plangeometriske figurer er:
Punkter
Et punkt har posisjon, men ingen utstrekning, det har altså dimensjon 0. Men vi må naturligvis gi et punkt en viss utstrekning når vi tegner det. Vi bruker vanligvis store bokstaver A, B, C, …, som navn på punkter, og markerer dem med en prikk, et kryss eller lignende.

Rette linjer
En rett linje har posisjon, retning og uendelig utstrekning. Linjer har dimensjon 1, det vil si at de ikke har bredde, selv om vi naturligvis må gi dem en viss bredde når vi tegner dem. Linjer gis vanligvis navn med små bokstaver l, m, n, …
Gitt to punkter A og B, finnes det nøyaktig én linje som går gjennom A og B. Denne noteres som l(A, B), «linja gjennom A og B» eller «linja AB».

Linjestykker
Et linjestykke er en del av ei linje som er begrenset av to endepunkter, A og B, nemlig den delen av linja gjennom A og B som ligger mellom A og B. Vi lar AB både betegne linjestykket fra A til B (eller fra B til A) og lengden av dette linjestykket, som kan defineres som avstanden mellom endepunktene. Det vil da framgå av sammenhengen hva som menes.

Stråler
En stråle er del av en linje som er bestemt ved et startpunkt og ved at den er ubegrenset i én av de to mulige retningene. Den har uendelig utstrekning. Hvis A er et endepunkt på en stråle og B er et punkt på strålen, snakker vi om strålen fra A gjennom B.
![]()
Vinkler
To linjer kan være plassert på forskjellige måter i forhold til hverandre: Enten har de ikke noen punkter felles og er parallelle, eller de skjærer hverandre i en vinkel. At to linjer, l og m, er parallelle skriver vi $l \parallel m$. Skriver vi $l \not \parallel m$, betyr det at linjene l og m ikke er parallelle, men skjærer hverandre.
En vinkel er en del av planet som er begrenset av to stråler med felles startpunkt. Dette startpunktet kalles vinkelens toppunkt. Hvis vinkelen er definert ved hjelp av strålen fra O gjennom A og strålen fra O gjennom B, skriver vi «vinkelen AOB» eller $\angle AOB$. Strålene OA og OB kalles vinkelens vinkelbein.
Hvis det bare er én vinkel med toppunkt i O, kan vi skrive $\angle O$ uten å bli misforstått. Eller vi kan gi vinkelen navn som u, v og w.

Vi markerer ofte vinkler med små sirkelbuer i ulike format, gjerne slik at vinkler som er like store, får samme format.

Vinkeltyper
En spiss vinkel er en vinkel som er mindre enn 90°.

En rett vinkel er en vinkel som er nøyaktig 90°.

En stump vinkel er en vinkel som ligger mellom 90° og 180°.

En like vinkel er en vinkel som er nøyaktig 180°.

En full vinkel er en vinkel som er nøyaktig 360°.
To vinkler som til sammen utgjør en like vinkel, kalles nabovinkler hvis de har et felles vinkelbein.
To vinkler med bein som er forlengelser av hverandre, kalles toppvinkler.
I figuren under er v og w, w og x, x og u, og u og v nabovinkler. v og x og u og w er toppvinkler.

Når vinkelen mellom to rette linjer, l og m, er rett, sier vi at l er en normal til m, eller at m er en normal til l.
To vinkler som til sammen utgjør en rett vinkel, er komplementvinkler til hverandre.

To vinkler som til sammen utgjør en like vinkel, er supplementvinkler til hverandre.

Nabovinkler er supplementvinkler med samme toppunkt og et felles vinkelbein imellom dem.

To vinkler som enten har venstre vinkelbein eller høyre vinkelbein felles, kaller vi samsvarende vinkler.
Samsvarende vinkler behøver ikke være like store.

Vinkelsammenhenger
Toppvinkler er like store.

Samsvarende vinkler er like store hvis og bare hvis de to overskårne linjene er parallelle.

To vinkler er like store hvis vinkelbeina er parvis parallelle.

Når vinkelbeina til to vinkler står parvis normalt på hverandre, er vinklene like.

Sirkler
En kurve i planet kan illustreres ved en strek på papiret, tegnet uten å løfte blyanten. En kurve kalles enkel hvis den ikke krysser seg selv.
![]()
En lukket kurve er en kurve uten endepunkter. Enhver enkel, lukket kurve deler planet i to områder, som kalles kurvens ytre og indre område.

En sirkel består av alle punkter i planet som har en gitt, fast avstand fra et bestemt punkt, sirkelens sentrum. Selve sirkelen omtales også som sirkelperiferien. Avstanden fra sentrum til periferien kalles sirkelens radius.
En sirkel er eksempel på en lukket kurve.

Omkretsen av en sirkel med radius r er gitt ved O = 2πr.
Arealet av en sirkel med radius r er gitt ved A = πr2.
En korde i en sirkel er et linjestykke med endepunkter på sirkelen. En diameter i en sirkel er en korde som går gjennom sirkelens sentrum. En radius i en sirkel er et linjestykke fra sentrum til et punkt på sirkelen, altså en halv diameter. En sekant er en rett linje som skjærer sirkelen. En tangent til sirkelen er en rett linje som har ett punkt – berøringspunktet eller tangeringspunktet, felles med sirkelen. Vi kan tenke på en tangent som grensestillingen for en sekant når de to skjæringspunktene nærmer seg hverandre. En bue er en del av sirkelperiferien.
Arealet av det indre området i en sirkel avgrenset av en korde kalles et segment, og arealet avgrenset av to radier kalles en sektor.
Disse begrepene er illustrert i bildene under:

Mangekanter
En mangekant, også kalt polygon, er en enkel, lukket to-dimensjonal kurve som består av rette linjestykker mellom like mange punkter i et plan. Dette betyr at mangekanten må ha minst tre hjørner. Under ser vi en enkel, men ikke lukket kurve, og en lukket, men ikke enkel kurve. Ingen av disse kurvene oppfyller derfor kravene til mangekanter.

Vi kan beskrive mangekanter ut fra kanter (sider), vinkler og hjørner. Forskjellen på hjørner og kanter er at kantene er selve linjestykket, mens hjørnet er der to linjestykker møtes:

En mangekant kalles konveks hvis alle linjer vi trekker mellom to vilkårlige punkter i mangekanten holder seg i det indre området. I en konveks mangekant er alle vinklene mindre enn 180°. Bildene under viser en konveks og en ikke-konveks mangekant. Vi ser at mangekanten som ikke er konveks har en vinkel som er større enn 180°, markert med rød pil, og at vi kan trekke linjer som går ut av det indre området, et eksempel vist med grønt.

I regulære mangekanter er alle sider like lange og alle vinkler like store. Bildet under viser en regulær trekant, firkant, femkant, sekskant, sjukant og åttekant.

Trekanter
Den enkleste mangekanten er trekanten, med tre hjørner og sider. Vi navngir gjerne en trekant etter hjørnene, for eksempel kalles en trekant med hjørner A, B og C for «trekanten ABC», noe vi også skriver som $\triangle ABC$.
Vinkelsummen i en trekant er alltid 180°.
Arealet av en trekant med grunnlinje g og høyde h er gitt ved $A=\frac{\displaystyle gh}{\displaystyle 2}$
Vi deler trekanter inn i flere typer etter egenskaper ved vinklene i trekanten:
-
- En spiss eller spissvinklet trekant er en trekant der alle vinklene er mindre enn 90°.
- En stump eller stumpvinklet trekant er en trekant der en av vinklene er større enn 90°.
- En rettvinklet trekant er en trekant der en av vinklene er 90°. De hosliggende sidene til den rette vinkelen kalles kateter, mens den motstående siden kalles hypotenusen.
- En likesidet trekant er en trekant der alle sidene er like lange. Også alle vinklene blir da like, nemlig 60°.
- En likebeint trekant er en trekant der to av sidene er like lange. To av vinklene blir da også like.
- En spiss eller spissvinklet trekant er en trekant der alle vinklene er mindre enn 90°.
Dette er illustrert i bildet under:

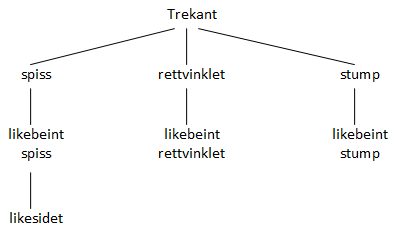
Vi kan plassere de forskjellige trekanttypene i et hierarki, slik:
Firkanter
Firkanten har, som navnet sier, fire hjørner og kanter. På samme måte som i en trekant navngir vi gjerne etter hjørnene, for eksempel kalles en firkant med hjørner A, B, C og D for «firkanten ABC», noe vi også skriver som $\Box ABCD$. Ei linje mellom to motstående hjørner i en firkant kalles en diagonal.
Vi deler firkantene inn i flere typer, der parallellitet, vinkler og sidelengden er definerende egenskaper:
-
- Hvis to par sider med felles vinkel er like lange, har vi en drake.
- Hvis to av sidene er parallelle, kalles firkanten for et trapes.
- Hvis to og to av sidene er parallelle, kalles firkanten for et parallellogram.
- Hvis alle sidene i et parallellogram er like, har vi en rombe.
- Hvis alle de indre vinklene i et parallellogram er rette, har vi et rektangel.
- Et rektangel der alle sidene er like, kalles et kvadrat.
- Hvis to par sider med felles vinkel er like lange, har vi en drake.
Dette er illustrert i bildet under:

I forrige avsnitt plasserte vi trekantene i et hierarki. Plasser firkantene i et tilsvarende hierarki.
Arealet av et parallellogram med grunnlinje g og høyde h, er gitt ved A = g · h.
Arealet av et trapes med to parallelle sider a og b, og høyde h, er gitt som $A=\frac{\displaystyle (a + b) \cdot h}{\displaystyle 2}$
-
- I et trapes er de to parallelle sidene henholdsvis 5 og 8 cm. Høyden er 6 cm. Hva er trapesets areal?
- Et trapes har areal 26 cm2. De to parallelle sidene er 7 og 6 cm. Hva er trapesets høyde?
Enhver polygon kan deles opp i trekanter. Dermed kan man i prinsippet beregne ethvert areal som er begrenset av rette linjer.

Arealet til en uregelmessig figur kan anslås. Elevene kan prøve å tegne arealet til hånda si på et blankt ark og legge transparenter med rutenett oppå tegningen av håndflaten. Så kan de telle ruter. Snakk om at hvis de kun teller rutene som ligger helt inni hånda, vil arealet bli for lite. Hvis de også teller ruter som hånda delvis ligger inni, vil arealet bli for stort. Jo tettere rutenettet er, jo mer nøyaktig blir målingen.

Hjørner og vinkler i mangekanter
Deler vi en firkant i to langs en av diagonalene, får vi to trekanter. Limer vi to trekanter sammen, får vi en firkant. Siden vinkelsummen i en trekant er 180°, blir derfor vinkelsummen i en firkant 360°.
Generelt, hvis vi har en n-kant og limer til en trekant, får vi en (n+1)-kant, der vinkelsummen har økt med 180°. For hvert hjørne utover tre en mangekant har, øker altså vinkelsummen med 180°, og vi har:
Vinkelsummen i en n-kant er
(n − 2) · 180°
I en regulær n-kant er alle vinklene like store. For en regulær n-kant gir derfor regelen over følgende korollar:
Hver vinkel i en regulær n-kant er
${\large \frac{ n – 2}{n}} \cdot 180^\circ$
Kilder
-
- Brodahl, C. (2016). Forkurs til MA-924 og MA-925. Upublisert manuskript, UiA.
- Hinna, K. R. C., Rinvold, R. A., Gustavsen, T. S. (2011) QED 5-10, bind 1. Høyskoleforlaget.


 Se film om periodisitet
Se film om periodisitet











 Last ned den tilhørende GeoGebra-fila
Last ned den tilhørende GeoGebra-fila